Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.4 - Ex. 10
Desenhe o gráfico de e de seu plano tangente no ponto dado. (Utilize um sistema algébrico computacional tanto para computar as derivadas parciais quanto para traçar os gráficos da função e de seu plano tangente.) Em seguida faça uma ampliação até que a superfície e o plano tangente se tornem indistinguíveis.
10-
Passo 1
E aí, pessoal! Beleza?
Nessa questão nós temos a função
Precisamos fazer o gráfico de , bem como do seu plano tangente no ponto
Para fazer o gráfico nós vamos usar um software para nos auxiliar. Para o caso do plano tangente, vamos precisar lembrar o que ele é e como nós obtemos. Aí depois disso fazemos o seu gráfico utilizando um software também.
Tranquilo? Então vamos lá...
Passo 2
Antes de começar a plotar gráficos, vamos lembrar como obter o plano tangente?
Suponha que tenha derivadas parciais contínuas. Uma equação do plano tangente à superfície no ponto é dada por
onde, no nosso caso, .
Agora que sabemos como obter a equação do plano tangente a , vamos às contas...
Passo 3
Utilizando o Symbolab, vemos que as derivadas parciais dessa função gigante são:
Uau, ainda bem que não precisa fazer isso na mão!
Precisaremos plotar a função e seu plano tangente que será igual a:
Aplicando o ponto nas derivadas parciais, temos:
Portanto, o plano tangente é
Passo 4
Agora, basta que a gente coloque as equações de e do plano tangente em um software para plotar os gráficos.
O gráfico da função e do plano tangente serão:
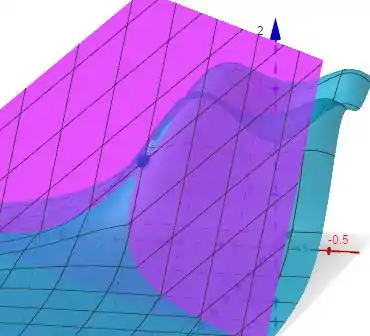
Aproximando no ponto temos:
Note que, quando damos zoom no gráfico de , o plano tangente cada vez mais se confunde com o gráfico de
Resposta
Gráficos no passo 4.