Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 1

Uma região R é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∫ R ∫ f x , y d A   como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .

1-

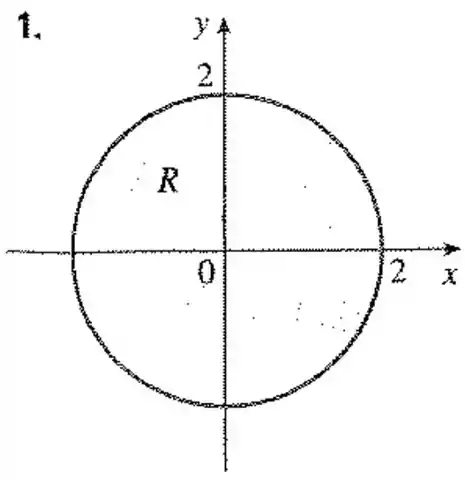
Passo 1

Olá, tudo bem?

Vamos entender melhor esse enunciado.

A região R mostrada é essa:

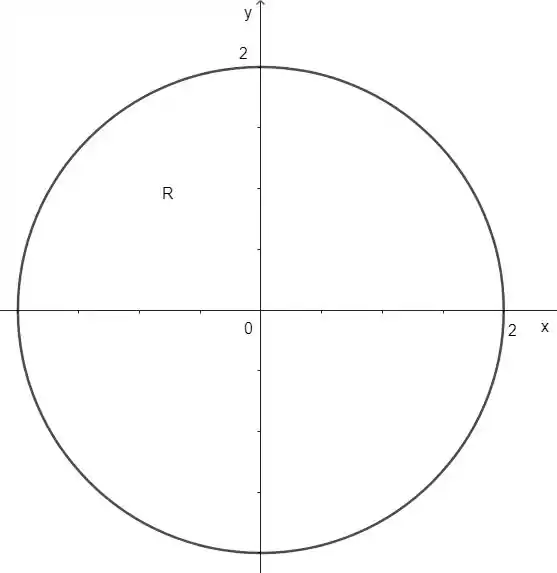
Com isso, a questão quer que montemos a integral

∫ R ∫ f x , y   d A  

como uma integral inteirada. Que significa colocar os limites nela e dizer a ordem de integração. Tipo assim:

∫ c d ∫ a b f x , y   d x d y

Aqui estou dizendo que a integral interna vai ser integrada em relação a d x e depois de resolvida, integraremos o que sobrar em relação a d y .

Você também pode pensar como uma integral dentro de uma integral:

∫ c d ∫ a b f x , y   d x d y

Sendo que f é qualquer função que seja contínua nesse círculo. Não precisaremos escrever uma função, apenas dizer quais os parâmetros de f , ok?

E escolher se devemos usar coordenadas polares r , θ

x = r cos ⁡ θ

y = r sen ⁡ θ

ou coordenadas retangulares x , y .

x = x

y = y

Lembrando que quando utilizamos coordenadas polares, devemos multiplicar a função f pelo jacobiano J , que sempre será igual a r nessas coordenadas!

Para resolver a questão, primeiro analisaremos quais coordenadas usar e depois montaremos a integral.

Tranquilo?

Passo 2

Então, primeiro vamos analisar a região R:

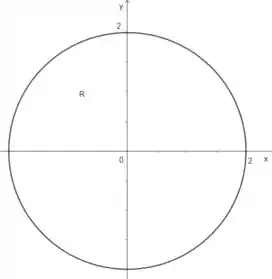
Por ser um círculo é melhor utilizar coordenadas polares, pois, já que a equação do círculo é

x 2 + y 2 = r 2

Se tentarmos isolar x , y envolverá raízes, e isso não será fácil de resolver.

Portanto, em coordenadas polares, temos.

x = r cos ⁡ θ

y = r sen ⁡ θ

Onde r é o raio do nosso círculo. E como ele está com o centro na origem, será 2 , como mostra a figura.

E θ é o ângulo que o raio percorre para formar o círculo, como o círculo dá uma volta completa, ele percorre 2 π . Tudo bem?

Caso o centro estivesse deslocado, teríamos que calcular esse raio de outra maneira. Show?

Passo 3

Agora vamos montar a nossa integral.

Vamos colocar primeiro a ordem de integração das variáveis,

d A = d θ d r

Poderia ser ao contrário também!

Então,

∫ R ∫ f x , y   d A   = ∫ R ∫ f x , y   d θ d r  

Agora vamos colocar os limites de integração:

∫ R ∫ f x , y   d θ d r   = ∫ 0 2 ∫ 0 2 π f x , y   d θ d r

Como d θ está na parte de dentro, temos que colocar o limite dele na integral de dentro.

E como d r está na parte de fora, colocamos o limite dele na integral de fora.

Agora precisamos substituir as variáveis da função f x , y . Sendo

x = r cos ⁡ θ

y = r sen ⁡ θ

Logo,

∫ 0 2 ∫ 0 2 π f x , y   d θ d r = ∫ 0 2 ∫ 0 2 π f r c o s   θ , r s i n   θ   d θ d r

E não podemos nos esquecer de colocar o Jacobiano!

∫ R ∫ f x , y d A   = ∫ 0 2 ∫ 0 2 π f r c o s   θ , r s i n   θ r   d θ d r

Prontinho!

Resposta

Usaremos coordenadas polares.

∫ 0 2 ∫ 0 2 π f r c o s   θ , r s i n   θ r   d θ d r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ - 1 1 ∫ - 1 - x 2 1 - x 2 2 1 + x 2 + y 2 d yd x
Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ 0 1 ∫ x 2 - x 2 x + 2 y d yd x
Nos Exercícios 23-26, esboce a região de integração e converta cada uma das integrais polares ou soma de integrais a uma integral cartesiana ou soma de integrais. Não calcule as integrais. ∫ 0 π 2 ∫ 0
Fórmula da área em coordenadas polares: Utilize a integral dupla em coordenadas polares para deduzir a fórmula: A = ∫ α β 1 2 r 2 d θ para a área da região em formato de leque entre a origem e a curva
Suponha que a área de uma região no plano de coordenadas polares seja A = ∫ π 4 3 4 π ∫ c o s s e c θ 2s e n θ rd rd θ Esboce a região e encontre sua área.