Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 55
Encontre o volume do sólido descrito. A base de é a região elíptica limitada pela curva . As secções transversais perpendiculares ao eixo são triângulos isósceles retos com hipotenusa na base.
Passo 1
Fala aí. Vamos matar mais essa questão juntinhos? Então partiu!
Queremos encontrar o volume do sólido onde a base é a região elíptica limitada pela curva:
Além disso as seções transversais da elipse perpendiculares ao eixo são triângulos isósceles retos com hipotenusa sendo a base desses triângulos.
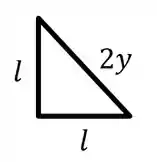
Se considerarmos que é uma aresta desse triângulo retângulo isósceles e é uma hipotenusa, então podemos aplicar o teorema de Pitágoras com:
O que nos dá a seguinte relação:
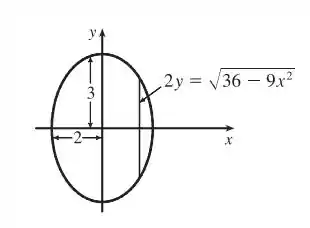
Agora vamos olhar a expressão da nossa elipse que é:
Temos a seguinte figura:
Veja que nela também podemos isolar o termo . E assim termos a seguinte figura:
Passo 2
O que estamos procurando é o volume do sólido descrito, lembrando que são infinitos triângulos isósceles que formam esse sólido e que suas hipotenusas estão sempre perpendiculares ao eixo varrendo a região da elipse.
Sendo assim iremos integrar a função destacada ao longo do eixo varrendo toda a região da elipse que se inicia no ponto e vai até o . A função que iremos integrar é a área dos triângulos formados.
Como temos uma simetria na elipse, podemos fazer a integral apenas de um lado e multiplicar por dois:
Como nosso triângulo é isóscele e reto sua área pode ser expressa por:
Passo 3
Encaixando essas informações na integral, ficamos com:
Cortamos os 2 que estão dentro da integral, e lembrando que , fazemos: