Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.9 - Ex. 14

Uma região R no plano x y é dada. Determine equações para a transformação   T que mapeia uma região retangular   S no plano u v sobre R , onde os lados de S são paralelos aos eixos u e v .

R é ligado pelas hipérboles y = 1 x ,   y = 4 x e pelas retas y =   x , y = 4 x no primeiro quadrante.

Passo 1

E aí, gente! Belezinha?

O enunciado diz que estamos numa região R no plano x y . Ok?

Ela está pedindo para determinar as equações dessa região ligada pelas hipérboles

y = 1 x

  y = 4 x

E pelas retas

y =   x

y = 4 x

Para podermos fazer a transformação T que mapeia uma região retangular S em um outro plano ( u ,   v ) que está sobre R , e os lados S são paralelos aos eixos u v .

Socorro, né? Mas calma.

Para o exercício em questão já temos as equações para cada lado da figura, precisamos encontrar os limites e uma forma de relacionar com u v manipulando as equações que já temos.

Passo 2

Vamos jogar no programa e montar o gráfico:

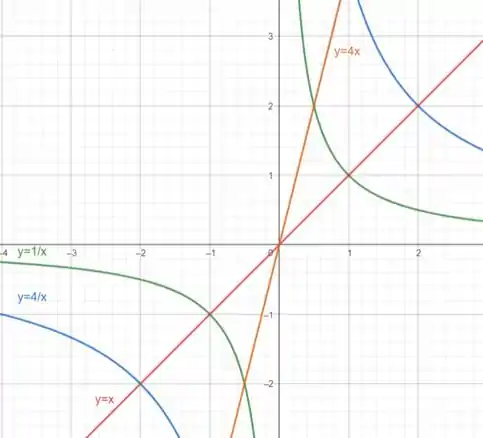
Podemos separar as curvas em 2 conjuntos: um conjunto com as hipérboles e um conjunto com as duas retas.

Dessa forma, temos que o primeiro conjunto, de hipérboles, será

y = 1 x → x y = 1

y = 4 x → x y = 4

Observa que há termos em comum?

Vamos fazer com que

u = x ⋅ y

Substituindo na equação, ficamos então com

u = 1

u = 4

Logo, temos que nosso u terá o intervalo de 1 ≤ u ≤ 4 .

Passo 3

Para v , vamos usar o segundo conjunto, o de retas, para encontrar quais serão seus limites

y = x → y x = 1

y = 4 x → y x = 4

Também temos termos em comum. Por isso, vamos chamar

v = y x

Assim, temos que seus limites serão

v = 1

v = 4

E nosso intervalo será:

1 ≤ v ≤ 4

Assim, plotando o gráfico, ficamos que nossa função em u v será

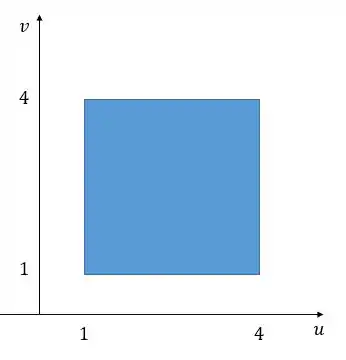
Show de bolaaa! 😊

Resposta

u = x y

v = y x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o sólido do Exercício 17(a) tiver densidade constante k , encontre seu momento de inércia em relação ao eixo z .Sólido delimitado pelo elipsoide x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 Transformação: x = a
Calcule ∭ E d V , onde E é o sólido delimitado pelo elipsoide x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 . Utilize a transformação x = a u , y = b v , x = c w .A Terra não é perfeitamente esférica; como resultad
Uma região R no plano x y é dada. Determine equações para a transformaçãoT que mapeia uma região retangularS no plano u v sobre R , onde os lados de S são paralelos aos eixos u e v R é o paralelogramo
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u - v , y = 1 4 v - 3 u