Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.9 - Ex. 12
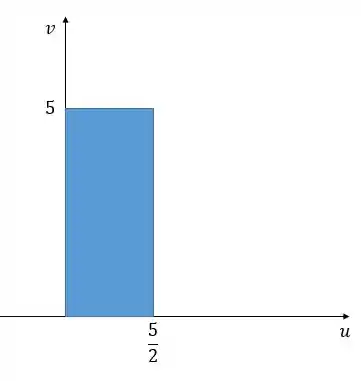
Uma região no plano é dada. Determine equações para a transformação que mapeia uma região retangular no plano sobre , onde os lados de são paralelos aos eixos e
é o paralelogramo com vértices (0, 0), (4, 3), (2, 4), (-2, 1).
Passo 1
Fala, gente bonita!
Olha só, estamos numa região no plano , show?
A questão pede para determinar as equações de um paralelogramo com vértices
Para podermos fazer a transformação que mapeia uma região retangular em um outro plano que está sobre , e os lados são paralelos aos eixos . Loucura, tontura!
Calma, respira e não pira!
Para o exercício em questão vamos precisar encontrar as equações de reta dos lados do paralelogramo e depois aplicar a transformação de para , analisando os novos limites para o novo plano.
Passo 2
Vamos começar calculando as equações para os lados do paralelogramo.
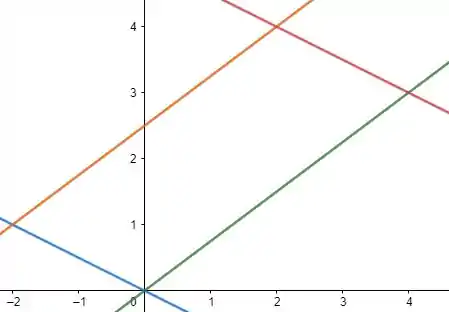
Temos que os dois pontos que podemos usar para a reta azul são . Assim, temos que nossa reta será dada por essa fórmula aqui:
Onde é um ponto qualquer por onde a reta passa e o coeficiente angular da
reta.
Calculando para os dois pontos que temos, chegamos que
E o ponto que iremos escolher será . Assim, nossa equação ficará sendo como
Passo 3
Para a reta laranja, iremos usar a mesma equação, porém agora com os pontos . Nossa inclinação da reta será aplicada na mesma fórmula que no passo anterior:
Selecionando qualquer dos dois pontos que passe pela reta, chegamos que nossa equação será
E fazendo o mesmo processo para a reta rosa e verde, chegamos que cada uma, respectivamente, será
E
Passo 4
Temos que as retas azul e rosa são parecidas, assim como as laranja e verde.
Podemos, então, separar em dois conjuntos.
No primeiro conjunto (azul e rosa) faremos uma modificação:
Podemos chamar então esse termo em comum de
Assim, a equação acima fica, com os pontos dos vértices dados na questão, ficaremos com
Fazendo o mesmo processo para o segundo conjunto de equações (laranja e verde), temos que agora
Assim, substituindo os pontos dos vértices, temos que
Assim, ficamos com o seguinte gráfico.
