Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.2 - Ex. 42

A região no primeiro quadrante limitado pela curva y = c o s x e pelas retas y = 1 e x = π 2 gira em torno do eixo x. Ache o volume do sólido gerado.

Passo 1

Bom, primeiro vamos esboçar a região para facilitar a visualização do problema:

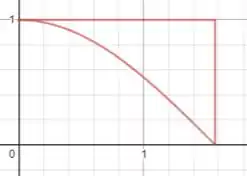
Como precisamos girar essa região em torno do eixo x, vamos usar a equação do volume pelo método dos discos:

V = π ∫ a b f x 2 d x

Passo 2

Como vamos integrar em x, os limites serão onde a reta x = π 2 e onde a curva começa, x = 0 , nossa f ( x ) será a equação da própria curva, nossa integral então fica assim:

V = π ∫ 0 π 2 c o s 2 x d x

Passo 3

Agora basta resolver a integral, vamos reescrever o cosseno ao quadrado através da identidade trigonométrica:

c o s 2 x = 1 + c o s 2 x 2

Ficamos com:

V = π ∫ 0 π 2 1 + c o s 2 x 2 d x

Colocando o 2 para fora e integrando cada termo:

V = π 2 x + s e n 2 x 2 π 2 0

Substituindo os limites:

V = π 2 π 2 + s e n 2 π 2 2

V = π 2 4

Resposta

V = π 2 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os volumes dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas nos Exercícios 19-28 em tomo do eixo x.20- y = x 3 , y = 0 ,x = 2
Nos Exercícios 15-18, determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo dado.15- Em torno do eixo x
Determine os volumes dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas nos Exercícios 19-28 em tomo do eixo x.19- y = x 2 , y = 0 ,x = 2
Nos Exercícios 15-18, determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo dado.17- Em torno do eixo y
Nos Exercícios 15-18, determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo dado.18- Em torno do eixo x