Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 3.7 - Ex. 7b

Representar graficamente os seguintes subconjuntos de R 2 . Identificar os conjuntos abertos.

{ x , y ∈ R 2 | x 2 - 4 x + y 2 ≥ 0 }

Passo 1

Galera, pra gente representar graficamente o conjunto, primeiro vamos dar uma ajeitada na equação dele, porque assim não dá pra concluir nada! O conjunto é:

{ x , y ∈ R 2 | x 2 - 4 x + y 2 ≥ 0 }

Então vamos mexer na equação:

x 2 - 4 x + y 2 ≥ 0

Completando o quadrado pro x :

x 2 - 4 x + 4 + y 2 ≥ 4

Arrumando,

x - 2 2 + y 2 ≥ 2 2

Então esse conjunto é a parte externa de uma circunferência de centro ( 2 ,   0 ) e raio 2 , contando com a bordinha por causa do sinal de igual. Como é uma parte externa, esse não é um conjunto aberto.

Passo 2

Representando graficamente:

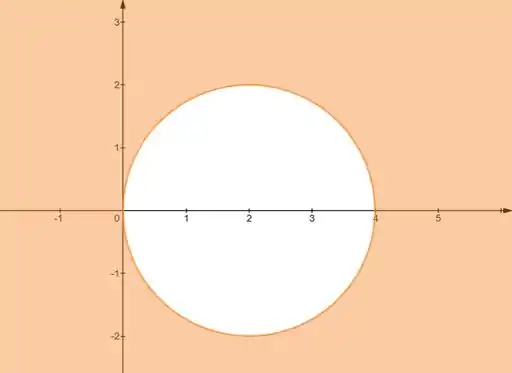
Resposta

Parte externa e borda de circunferência em R 2 , de centro ( 2 ,   0 ) e raio 2 . Não é conjunto aberto.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhar algumas curvas de nível e esboçar o gráfico:(l) z = 4 - x 2
Desenhar algumas curvas de nível e esboçar o gráfico:(o) z = 1 4 x 3
Desenhar algumas curvas de nível e esboçar o gráfico:(q) z = 3 y 2 - 2 x 2
Desenhar algumas curvas de nível e esboçar o gráfico:(o) z = 2 x 2 - 3 y 2
Encontrar a curva de interseção do gráfico da função dada com os planos dados, representando graficamente:(a) z = x 2 + y 2 com os planos z = 1 ; x = 1 ; y = 1 .