Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 3.7 - Ex. 10a
Identificar as afirmações verdadeiras:
a) é ponto de acumulação do conjunto .
Passo 1
Vamos começar a análise relembrando o conceito de ponto de acumulação. A definição de um ponto de acumulação é a seguinte: um ponto é ponto de acumulação de quando existirem pontos de que estejam tão próximos de quanto desejarmos. Isso é uma definição engraçada pra gente que gosta das coisas na prática hahahah. Ó, vamos seguir com a seguinte regra de bolso: um ponto vai ser de acumulação quando ele estiver ou dentro da figura ou na bordinha dela. Assim tá mais fácil de gravar, né? hahahah
Passo 2
Então, nessa questão a gente quer saber se o ponto é ponto de acumulação de . Vamos ver! Essa inequação pode ser representada assim:
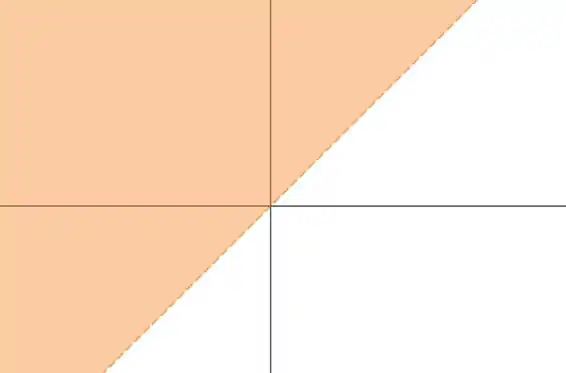
Bom, daí já dá pra gente ver que o ponto não está dentro da região que a gente tá tratando, mas ele tá na bordinha, né, porque a reta ela só dá uma passada por ele! Dessa forma, a gente pode dizer que o ponto é sim de acumulação! Verdadeira!
Resposta
Verdadeira.