Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.2 - Ex. 1e
Represente geometricamente o campo vetorial dado.
e)
Passo 1
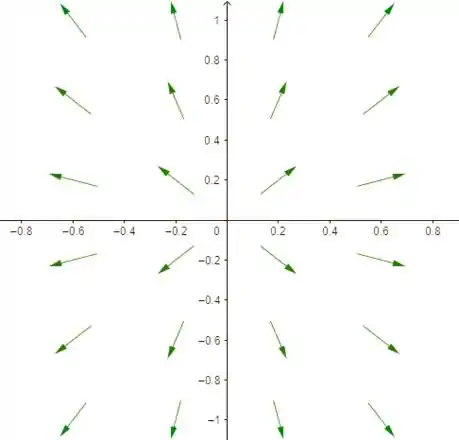
Vamos fazer a norma desse vetor para ver a intensidade do campo vetorial.
Beleza, a intensidade do campo vetorial então é constante e igual a 1.
Temos também que é normal à circunferência de centro na origem e que passa pelo ponto . Daí, o desenho do campo vetorial é:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
2 ) Considere o campo vetorial F ( x ,y )=i +( x-y ) j . Desenhe F(x, y) nos pontos da reta a )y=x
2 ) Considere o campo vetorial F ( x ,y )=i +( x-y ) j . Desenhe F(x, y) nos pontos da reta b )y=x-1
2 ) Considere o campo vetorial F ( x ,y )=i +( x-y ) j . Desenhe F(x, y) nos pontos da reta c )y=x-2
3 ) Considere o campo vetorial g ( x ,y )=i +x y j . Desenhe g(x,y) nos pontos da hipérbole xy = 1, com x0
Calcule o trabalho realizado pelo campo de forças F x , y = ( x 2 - y 2 , 2 x y ) ao mover uma partícula ao longo da fronteira do quadrado limitado pelos eixos coordenados e pelas retas x = a e y = a