Represente graficamente as equações dos Exercícios 9-58 seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflexão.

35-

Agora fazendo a primeira derivada dessa função nós temos:

O que nos dá:

Agora fazendo a segunda derivada temos:

Agora precisamos descobrir seus pontos de concavidade pra isso precisamos fazer

Cortando temos :

Elevando-se ao cubo:

Logo satisfaz a igualdade logo ela representa uma concavidade.

E dividindo por para diferente de 0,

Logo temos uma concavidade em .

Logo encontramos:

Agora precisamos descobrir o y associado a esses valores de .

Para ;

Para ;

Logo temos como pontos críticos:

Agora precisamos descobrir se esses pontos são máximo ou mínimo local e se existe pontos de inflexão:

Para achar os pontos de máximo e mínimo precisamos substituir os valores previamente encontrados na derivada segunda:

Para temos:

Como o teste de derivada segunda no ponto (0,0) deu 0 assim como o teste da derivada primeira, assumimos que não sabemos como se comporta a função nesse ponto logo ela pode ser um ponto de singularidade, ponto máximo ou mínimo local, enfim qualquer coisa. O que garantirá é como a função se comportará antes e depois desse ponto.

Agora para

Já que deu negativo, podemos dizer que o ponto (1,) é máximo local

Agora para encontrarmos os pontos de inflexão precisamos ver se a derivada segunda dá zero sem com que ele tenha derivada primeiro também.

Cortando o denominador 9 e passando uma das parcelas pro outro lado temos:

Agora passando os números pro lado direito e as variáveis pro esquerdo temos e adotando diferente de zero:

Logo:

Descobrindo a posição desse ponto temos:

O que é igual a :

Agora precisamos ver se a função tem assíntotas, para isso fazer o limite dessa função para

Se fizermos essa conta acharíamos :

; que não é uma indeterminação .

Logo do ponto até infinito a função somente desce

Agora para menos infinito temos:

Se fizermos a multiplicação dos limites encontraremos:

Onde na primeira parcela elevaremos um número negativo ao quadrado e na segunda elevando a quinta. Na primeira muda o sinal na outra não ficando:

Agora precisamos organizar nossos pontos e seus resultados para podermos ver se tem concavidade para cima ou para baixo. Substituindo pontos nas suas derivadas.

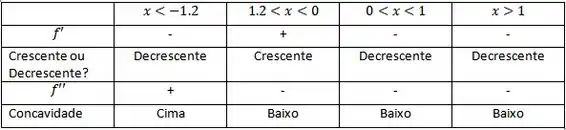
Exemplo:

Para testar a concavidade no ponto -1 vou aplicar esse ponto na sua derivada segunda:

Como deu positivo a concavidade é para cima

Como antes do ponto a função é decrescente com concavidade para baixo e após ela a função assume uma trajetória crescente com a mesma concavidade para baixo, a função exatamente nesse ponto forma um bico. Então dizemos que nesse ponto a função tem uma singularidade.