Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.4 - Ex. 3

  1. Identifique os valores de equilíbrio. Quais são estáveis e quais são instáveis?
  2. Construa a reta de fase. Identifique os sinais de y' e y".
  3. Esboce várias curvas integrais.

d y d x = y 3 - y

Passo 1

  1. Pra começar, y 3 - y = y y 2 - 1 = y ( y - 1 ) ( y + 1 ) .

    2. Os valores de equilíbrio são onde a derivada é zero, ou seja, y = 0 e y = 1 e y = - 1 .

    Veja que a derivada vai ser negativa em - ∞ ,   - 1   e entre ( 0,1 ) . Nos intervalos de ( - 1,0 ) e ( 1 , ∞ ) ela é positiva.

    Ou seja, os valores vão sempre se afastar de - 1   e 1 e se aproximar de 0 .

    Com isso, temos que y = 0 é um valor estável e y = - 1 e y = 1 são valores instáveis da função.

    Passo 2

  2. Vamos calcular a derivada segunda:

    3. y ' ' = d d x y ' = d d x ( y 3 - y )

    y ' ' = ( 3 y 2 - 1 ) y '

    y ' ' = 3 y 2 - 1 y 3 - y = y ( 3 y 2 - 1 ) ( y - 1 ) ( y + 1 )

    Então, y ' ' muda de sinal em y = 0 , y = - 1 3 , y = 1 3 e y = - 1 e y = 1 .

    Então, montamos a reta de fases:

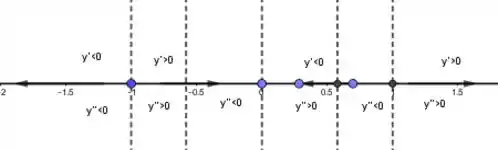
    Passo 3

  3. Para esboçar as curvas integrais, precisamos descobrir a integral.

Como a derivada d y d x = y 3 - y = y ( y 2 - 1 ) , vamos fazer:

d y y ( y 2 - 1 ) = d x

Temos que integrar os dois lados. Dá pra fazer de várias formas, mas vamos fazer assim:

- 1 2 ln ⁡ y 2 + 1 2 y 2 - 1 = x + C

Beleza, agora a gente tem isolar o y ...

1 2 ln ⁡ y 2 - 1 y 2 = x + C

Usamos a exponencial dos dois lados...

y 2 - 1 y 2 = e 2 x + C

y 2 1 - e 2 x + 2 C = 1

y 2 = 1 1 - e 2 x + 2 C

Podemos fazer e 2 C = K :

y 2 = 1 1 - K e 2 x

Essa é a nossa família de integrais. Para esboçarmos as curvas integrais, é só marcarmos as retas de fase e alternamos o valor de K na integral.

Usando alguns valores, como K = ± 1 ,   ± 2 , ± 3 .   Temos as curvas integrais:

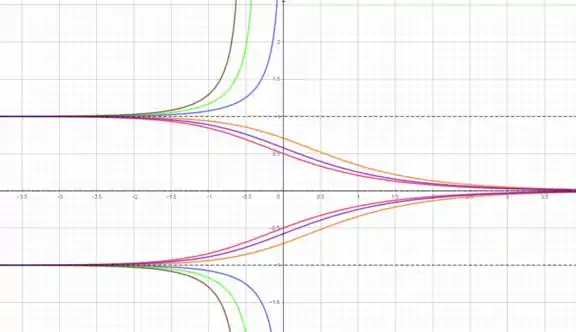
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um circuito elétrico simples consiste em um resistor de R ohms, onde R = 1 + 0,001t em ts com t variando entre [0,500]. O resistor é ligado em serie com o capacitor de 0,1 farad e uma força eletromotr
Um circuito elétrico simples consiste em um resistor de R ohms, onde R = 1 + 0,001t em ts com t variando entre [0,500]. O resistor é ligado em serie com o capacitor de 0,1 farad e uma força eletromotr
Uma mulher derruba o seu binóculo estando num balão a 150 m do solo, que está subindo com uma velocidade de 10m / s . (a) Quanto tempo irá decorrer até o binóculo atingir o solo e qual a velocidade es
Uma pedra é atirada para cima, partindo do solo, com uma velocidade inicial de 25m / s . (a) Quanto tempo irá decorrer até que ela retorne ao solo? (b) Qual a velocidade escalar quando ela atinge o so
Uma pedra é atirada verticalmente para cima, partindo do solo, com uma velocidade inicial de 15m / s . (a) Por quanto tempo ela subirá? (b) Qual a altura máxima atingida pela pedra?