Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.6 - Ex. 22
22. Resolva a equação diferencial e use uma calculadora ou um computador para traçar vários membros da família de soluções. Como a curva solução muda quando varia?
Passo 1
A EDO é linear com e .
Passo 2
Lembrando que o fator integrante é dado por , ou seja, .
Passo 3
Sabendo que dado o fator integrante , a solução é dada por . Já sabemos que e que .
Passo 4
Então precisamos calcular . Fazendo , temos que , isto é, . Então temos . E então a solução é e portanto, .
Passo 5
Variando nos números e (reta ) e em , temos a seguinte família de soluções:
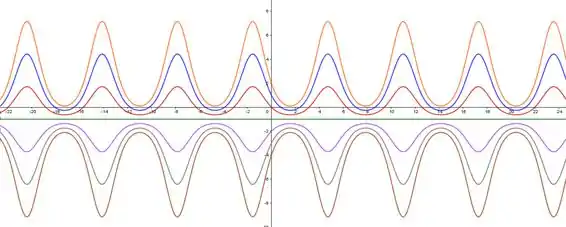
Resposta
Observando o gráfico, notamos que quando é negativo, as soluções estão abaixo da reta e quando é positivo, a curva fica acima da reta .
Exercícios de Livros Relacionados
Corrente em um circuito RL desligado Se o interruptor de um circuito RL for desligado depois de a corrente atingir o valor estacionário I = V / R , o decaimento da corrente ( esboçado graficamente aqu
Resolva os problemas de valor inicial nos Exercícios 15-20: d y d x - x y = x y ( 0 ) = - 6
Dedução da Equação 7 no Exemplo 4b.Em seguida, use a condição inicial i 0 = 0 para determinar o valor de C. Isso completará a dedução da Equação 7.
Dedução da Equação 7 no Exemplo 4a. Mostre que a solução da equação d i d t + R L i = V L seria: i = V R + c e - R L t
Dedução da Equação 7 no Exemplo 4c.Mostre que i = V / R é uma solução da Equação 6, e que i t = c e - R L t satisfaz a equação: d i d t + R L i = 0 Equação 6) d i d t + R L i = V L