Outro modelo para a função crescimento para uma população limitada é dado pela função de Gompertz, que é uma solução da equação diferencial

onde é uma constante e é a capacidade de suporte.

(a) Resolva essa equação diferencial.

(b) Calcule .

(c) Trace a função de crescimento de Gompertz para e , e compare-a com a função logística no Exemplo . Quais são as similaridades? Quais são as diferenças?

(d) Sabemos do Exercício que a função logística cresce mais rapidamente quando . Use a equação diferencial de Gompertz para mostrar que a função de Gompertz cresce mais rápido quando .

(b) Agora vamos calcular o limite:

Então, depois de algum tempo, a solução sempre tende à sua capacidade de suporte, beleza?

(c) Com as constantes fornecidas pelo enunciado, queremos traçar a seguinte função de Gompertz:

Também, para comparar, vamos traçar a função logística do Exemplo :

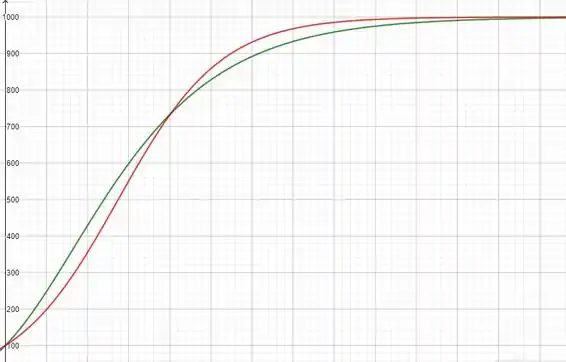
Em verde, a função de Gompertz; em vermelho, a função logística do Exemplo

Algumas semelhanças entre essa curvas são que elas começam do mesmo ponto (pois para ambas) e tendem à mesma solução de equilíbrio .

Uma diferença entre elas é que elas tem diferentes pontos de inflexão, ou seja, a concavidade delas não muda nos mesmos pontos.

(d) Para descobrir onde a função de Gompertz cresce mais rápido, precisamos maximizar a sua derivada. Ou seja, precisamos maximizar a função .

Lembra de como maximizamos uma função? Primeiro temos que achar os pontos críticos, derivando a função e igualando a , olha só:

Mas, a partir da equação diferencial, sabemos quem é

Lembre-se de usar a regra do produto e da cadeira quando for derivar, heim?

Vamos considerar , pois isso nos daria uma taxa de crescimento nula, sendo que queremos maximizá-la. Então podemos “cortar” da nossa equação:

Então achamos esse ponto crítico, mas ainda não podemos dizer que ele nos dá o máximo da função, pois ainda teríamos que analisar os extremos do domínio: e ( não é ponto do domínio pois anularia o denominador da fração , presente na função que queremos maximizar) .

Se descobríssemos, por exemplo, que ou nos dá uma taxa de crescimento maior do que a do ponto crítico , nem poderíamos dizer que existe um máximo global, pois nem nem são realmente pontos, o que significa que o intervalo é aberto. E lembre-se que não tem nenhum teorema que garante a existência de máximos ou mínimos globais num intervalo aberto.

Mas, pra nossa sorte, nem nem nos retorna valores maiores do que nos retorna para . Se usarmos algumas regrinhas de limite vamos ver que:

Então, é maior para , está provado.