Resolva a inequação.
Passo 1
Olá, galerinha! Em outras palavras, o que a questão pede é para estudarmos o sinal da expressão. Para isso, vamos analisar o numerador e o denimonador separadamente!
Mas antes disso, vamos mexer um pouco na nossa expressão para verificarmos quando ela será positiva ou negativa.
Para isso, vamos passar o para o outro lado:
Agora vamos fazer a essa subtração,
Ajeitando a expressão, ficamos com
Pronto! Agora vamos estudar o sinal dessa inequação.
Passo 2
Para estudar o sinal da expressão vamos analisar o numerador e o denimonador separadamente:
Para o numerador temos:

Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Para o demonimador temos:

Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Passo 3
Vamos lá, para resolver a inequação vamos analisar as duas imagens que achamos no passo anterior:
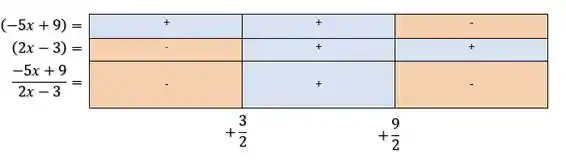
Temos que , ou seja, o resultado será negativo, quando o numerador e o denominador tiverem sinais opostos. Analisando as duas imagens vemos que isso acontece quando:
Lembre-se aqui que não incluímos o valor , pois a expressão não assume valor nesse ponto.
Resposta
para e