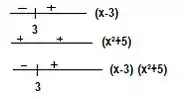Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.2 - Ex. 13e
Resolva a inequação
Passo 1
Olá, tudo bem? Vou ajudar vocês nessa questão. Como temos uma multiplicação de dois fatores, precisamos fazer o estudo dos sinais separadamente para depois analisar a multiplicação. Lembrando que a multiplicação de dois fatores de sinais iguais dá um resultado positivo, sinais diferentes dá um resultado negativo:
Ok?
Passo 2
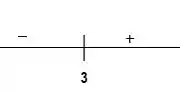
Analisando o sinal de :
Então temos uma mudança de sinal em . Agora vamos ver em torno:
- Antes de , por exemplo em :
- Depois de , por exemplo em :
temos que a função assume valores negativos.
temos que a função assume valores positivos.
Passo 3
Agora analisando o fator . Resgatando o resultado do problema temos que se um polinômio de segundo grau do tipo tiver , então o sinal da equação será dado pelo sinal do coeficiente .
Vamos confirmar se o é mesmo negativo:
Beleza! Então temos que o sinal de toda equação será dado pelo coeficiente .
Nesse caso temos que , então temos que . Sendo assim, concluímos que é maior do que zero independente do valor de .
Passo 4
Agora vamos combinar os resultados:
Antes de , o primeiro fator é negativo e o segundo é positivo, logo a multiplicação deles resultará em um valor negativo
Depois de , ambos fatores assumem valores positivos, então a multiplicação deles resultará em um valor positivo.
O intervalo d