Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.2 - Ex. 11a
11. Resolva a inequação
a)
Passo 1
E aí meus queridos! Temos uma questãozinha de inequação pra resolver!
Pra resolver a inequação de grau, que é nosso caso aqui, a dica é: vamos começar resolver a equação de grau correspondente, ou seja...
Depois, obtidas as raízes da equação, podemos fazer um graficozinho dessa equação e a partir daí, fazer o que a gente chama de estudo do sinal.
Assim, a gente pode descobrir numa boa quando essa equação é menor que zero, que é o que a gente tá procurando aqui...
Mão na massa!
Passo 2
Bom! Vamos começar descobrindo as raízes da equação abaixo...
Ora bolas! Como é uma equação do grau, ela possui duas raízes. E pra achá-las, usando a fórmula de Bhaskara:
Para aplicar a fórmula, temos que identificar os nosso coeficientes. A equação do grau, vem no formato
Sendo assim, os nossos coeficientes são
Substituindo na fórmula de Bhaskara, temos:
Resolvendo essa igualdade, temos que
Agora vamos esboçar o gráfico!
Passo 3
O gráfico de um polinômio de segundo grau só pode ser uma parábola com concavidade para cima ou para baixo. Isso depende do valor de . Se é positivo, o gráfico tem concavidade voltada para cima. Se negativo, a concavidade é para baixo.
No nosso caso, . Logo, a concavidade é voltada para cima...
Marcando os pontos encontrados para as raízes, e , e achando o ponto onde , temos
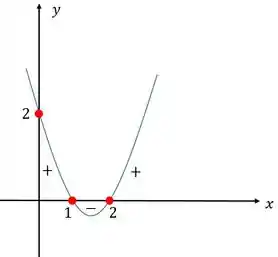
Repara que ele vai ter sinal positivo para valores de menores que e maiores que . Já a região negativa está entre e .
Logo, concluímos que o seguinte intervalo que satisfaça a nossa inequeção é:
E pronto! Terminamos aqui!