Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.3 - Ex. 3m
Resolva as inequações.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente resolver a inequação que ele nos deu. Isso significa que precisamos encontrar os valores de que satisfaçam a desigualdade.
Como nessa inequação estamos trabalhando com módulos, vamos relembrar a definição de módulo pra entender como resolver essa questão:
Repare que essa é uma função definida por partes e que cada expressão tem um sinal diferente. Então, o que nós vamos fazer é analisar o comportamento da função em cada parte, estudando seu sinal e verificando o que acontece com a nossa desigualdade.
Vamos lá!
Passo 2
Nossa inequação é dada por:
Vamos analisar os sinais das expressões separadas dentro dos módulos:
Para temos:
Vamos analisar o sinal antes e depois do ponto :
A expressão assume valores negativos quando e assume valores positivos quando .
Para temos:
Vamos analisar o sinal antes e depois do ponto :
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Passo 3
Vamos analisar as duas imagens que achamos no passo anterior:
Vamos analisar os três casos, com , e .
Com temos que e , assim vamos substituir as expressões na inequação com o sinal negativo:
Como estamos supondo , todo satifazendo a condição é solução da inequação, assim não é solução.
Passo 4
Com temos que e , assim vamos substituir a primeira expressão na inequação com o sinal negativo e a segunda com sinal positivo:
Fazendo o jogo de sinais:
Isolando :
Divididindo ambos os lados por :
E multiplicando por , invertemos o sinal da desigualdade:
Aqui, como estamos supondo , e está dentro da suposição, vamos usar ela. Assim todo satifazendo a condição é solução da inequação.
Passo 5
Por último com temos que e , assim vamos substituir as expressões na inequação com o sinal positivo:
Como estamos supondo , não está dentro dessa suposição, assim não existe que seja solução da inequação.
Juntando então as soluções do passo e vamos ter:
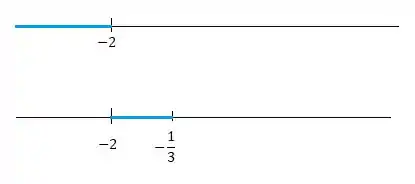
Assim juntando as duas temos como solução , pois fica dentro dessa solução.
Valeu, galera. Até a próxima! 😉