Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.4 - Ex. 12
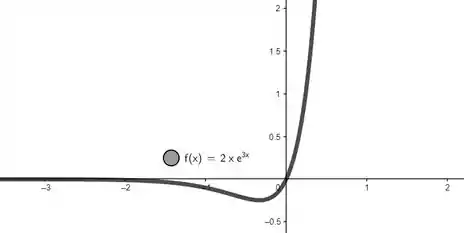
Resolva o problema de valor inicial dado. Esboce o gráfico da solução e descreva seu comportamento quando t cresce.
Passo 1
Primeiro temos que encontrar as raízes da equação usando a fórmula de Bhaskara. Vamos transformar essa equação em uma equação do 2º grau. Então passa a ser , a ser , e é o termo independente.
Sendo: .
Então para encontrar o usamos a fórmula de Bhaskara.
Importante!!!
- Se o resultado do , teremos raízes reais diferentes, e a equação característica vai ser:
- Se o resultado do , teremos raízes reais iguais, e a equação característica vai ser:
- Se o resultado do , teremos raízes complexas, e a equação característica vai ser:
Com isso em mãos vamos substituir na fórmula de Bhaskara:
Passo 2
Como a solução é:
Substituindo os valores das raízes e levando em consideração que nossa resposta está em função de e não de :
Falta achar o valor dessas constantes!
Passo 3
Agora vamos descobrir o valor das constantes através do valor inicial dado. Seja:
Teremos:
E seja:
Teremos:
Nossa solução geral será então:
E seu comportamento gráfico é:
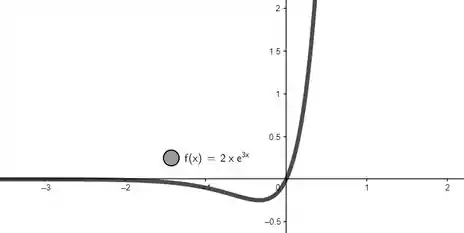
Resposta
