Enunciado
Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.7 - Ex. 16
- Será igual a para algum ? Justifique sua resposta.
- Use o método de Newton para determinar onde isso ocorre.
Passo 1
Queremos saber se existe algum valor de tal que . Usaremos o método de Newton que nos diz que
Para obtermos aproximações para as raízes da equação dada, caso ela exista.
Passo 2
Plotando o gráfico de obtemos
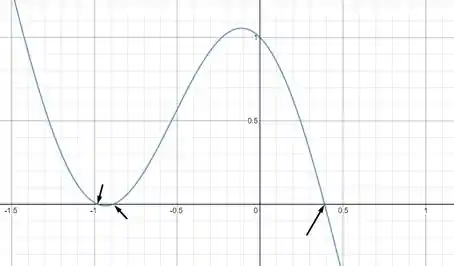
E podemos observar a presença de 3 raízes indicadas pelas setas.
Passo 3
Para utilizarmos o método de Newton, precisaremos derivar nossa função. Assim,
Dessa forma, nossa fórmula do método de Newton ficará
Como buscamos encontrar 3 raízes, necessitaremos de 3 valores iniciais, observando o gráfico acima vemos que as raízes se encontram próximas a e, então, tomaremos esses valores como valores iniciais e substituiremos na fórmula acima para encontrarmos as aproximações.
Resposta
As aproximações das raízes de são .
Exercícios de Livros Relacionados
As curvas y=x 2 ( x+1 ) e y= 1 x( x0 ) se cruzam em um ponto x=r . Use o método de Newton para estimar o valor de r com quatro casas decimais.
A figura a seguir mostra um círculo de raio r com uma corda de comprimento 2 e um arco s de comprimento 3 . Use o método de Newton para resolverr e θ (radianos) com quatro casas decimais. Suponha que
Para que valor(es) de x obteremos c o sx =- x ?
Para que valor(es) de x teremos e - x 2 = x 2 - x + 1 ?
Nos problemas para localizar submarinos, normalmente é necessário determinar o ponto de aproximação máxima (PAM) em relação a uma sonoboia ( equipamento eletrônico flutuante que capta sinais sonoros d