Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 42

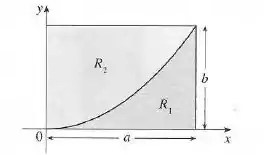
Um retângulo R com lados a e b foi dividido em duas partes R 1 e R 2 por um arco de parábola que tem seu vértice em um dos cantos de R e passa pelo canto oposto. Encontre os centroides de ambas as regiões R 1 e R 2 .

Passo 1

Beleza galera?! Yuri aqui e estarei te ajudando a resolver essa atividade.

Nesse exercício queremos encontrar o centroide das regiões especificadas. Para isso, utilizaremos os conceitos estudados de centroide por integração para encontrar a posição exata.

Por definição os centroides são dados por:

𝑥 ¯ = 1 𝐴 ∫ 𝑥 1 𝑥 2 𝑥 𝑓 �� 𝑑 𝑥

𝑦 ¯ = 1 2 𝐴 ∫ 𝑥 1 𝑥 2 𝑓 𝑥 2 𝑑 𝑥

Sendo A a área da região que queremos encontrara o centroide.

Passo 2

A parábola possui equação y = k x 2 e passa por a ,   b , então b = k a 2 . Podemos escrever

k = b a 2

y = b a 2 x 2

A área de R 1   será

A = ∫ 0 a b a 2 x 2 d x = b 3 a 2 x 3 0 a = a b 3

Podemos então encontrar o centroide para R 1

x 1 - = 1 A ∫ 0 a x b a 2 x 2 d x = 1 A b 4 a 2 x 4 0 a = 3 4 a

y 1 - = 1 A ∫ 0 a 1 2 b a 2 x 2 2 d x = 3 b 2 a 5 1 5 x 5 0 a = 3 10 b

Dessa forma, para a região 1 temos

x 1 - ,   y 1 - = 3 4 a ,   3 10 b

Passo 3

Para a região R 2 , temos

A área da região 𝑅 2 é dada pela subtração da área do retângulo pela área de 𝑅 1 :

𝐴 2 = 𝑎 𝑏 − 𝑎 𝑏 3 = 2 𝑎 𝑏 3

x 2 - = 1 A ∫ 0 a x b - b a 2 x 2 d x = 3 2 a x 2 2 - x 4 4 a 2 0 a = 3 8 a

y 2 - = 1 A ∫ 0 a 1 2 b 2 - b a 2 x 2 2 d x = 3 b 4 a x - 1 5 a 4 x 5 0 a = 3 5 b

Resposta

x 1 - ,   y 1 - = 3 4 a ,   3 10 b

x 2 - ,   y 2 - = 3 8 a ,   3 5 b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Avalie a integral e interprete-a como a área de uma região. Esboce a região ∫ - 1 1 | 3 x - 2 x | d x
Esboce a região delimitada pelas curvas fornecidas. Decida se quer integrar com relação a x ou y . Desenhe um retângulo aproximado típico e identifique sua altura e largura. Então, encontre a área da
Esboce a região delimitada pelas curvas fornecidas. Decida se quer integrar com relação a x ou y . Desenhe um retângulo aproximado típico e identifique sua altura e largura. Então, encontre a área da
Use um gráfico para encontrar as coordenadas x aproximadas dos pontos de interseção das curvas dadas. Então indique (aproximadamente) a área da região delimitada pelas curvas. y = 1,3 x ,y = 2 x
Esboce a região delimitada pelas curvas fornecidas e encontre sua área. y = 2 x 3 , y = x 2 / 8, 0 ≤ x ≤ 6