Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.1 - Ex. 36
Avalie a integral e interprete-a como a área de uma região. Esboce a região
Passo 1
Esboçando a região em um software matemático vamos obter
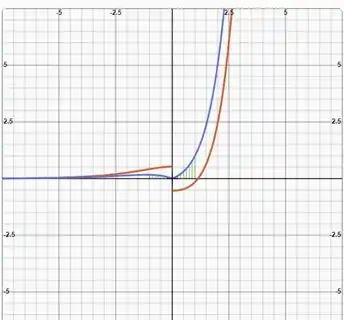
Assim, nossa integral pode ser calculada numericamente com
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. x = 1 / 2 ,x = yey = - x + 2
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = x 2 6ey = 6
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. x + y = 3ey + x 2 = 3
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. x = y 2 ,y - x = 2 ,y = - 2ey = 3
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y 2 = 2 xex 2 = 2 y