Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 39

Demonstre que o centroide de qualquer triângulo está localizado no ponto de intersecção das medianas. [Sugestão: Coloque os eixos de maneira que os vértices sejam a ,   0 , 0 ,   b e c ,   0 . Lembre-se de que uma mediana é um segmento de reta ligando um vértice ao ponto médio do lado oposto. Lembre-se também de que as medianas se interceptam em um ponto a dois terços da distância de cada vértice (ao longo da mediana) ao lado oposto.]

Passo 1

Bom galera, nesse exercício estamos interessados em demonstrar que o centroide de qualquer triângulo se encontra no ponto de interseção das medianas. Para isso, utilizaremos as definições de centroide.

Passo 2

Seguindo a sugestão, temos

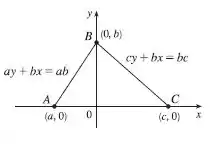
Calculando x - , temos

x - = 1 A ∫ a 0 x b a a - x d x + 1 A ∫ 0 c x b c c - x d x

Resolvendo a integral, temos

x - = b a A 1 2 a x 2 - 1 3 x 3 a 0 + b c A c x 2 2 - x 3 3 0 c = a + c 3

Passo 3

Calculando y - , temos

y - = 1 A ∫ a 0 1 2 b a a - x 2 d x + 1 A ∫ 0 c 1 2 b c c - x 2 d x

Resolvendo a integral, temos

y - = 1 A b 2 2 a 2 a 2 x - a x 2 + x 3 3 a 0 + 1 A b 2 2 c 2 c 2 x - c x 2 + x 3 3 0 c = b 3

Resposta

O centroide se encontra em a + c 3 ,   b 3 que é a interseção das medianas.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Comparando áreas, mostre que ln ⁡ 21ln ⁡ 3 .Deduza que 2e3 .
Comparando áreas, mostre que 1 2 + 1 3 + … + 1 nln ⁡ n1 + 1 2 + 1 3 + … + 1 n - 1
Use um gráfico para encontrar as coordenadas aproximadas de x dos pontos de intersecção das curvas dadas. Encontre a área de uma região limitada pelas curvas. y = x 4 y = 3 x - x 3
Use um gráfico para encontrar as coordenadas aproximadas de x dos pontos de intersecção das curvas dadas. Encontre a área de uma região limitada pelas curvas. y = x 2 y = 2 cos ⁡ x
Calcule a integral, interpretando-a em termos das áreas. ∫ 0 10 x - 5 d x