Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.1 - Ex. 23
Esboce a região delimitada pelas curvas fornecidas e encontre sua área.
Passo 1
Para esboçarmos a região delimitada pelas curvas vamos esboçar ambas as curvas em um mesmo gráfico e, assim, vamos obter
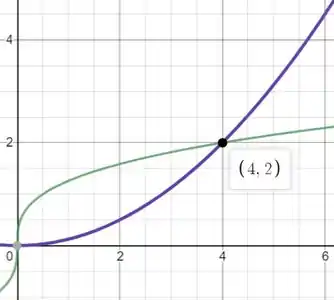
Ao plotarmos ambas as curvas em um mesmo gráfico já conseguimos obter o ponto de intersecção das mesmas. Para esse caso em específico vamos necessitar separar nossa integral em duas partes no intervalo dado, pois em uma parte temos uma função por cima e em outra temos outra função por cima e para encontrarmos a área necessitamos colocar no integrando a função de cima menos a de baixo. Assim, nessa situação vamos ter
Passo 2
Com a fórmula acima em mãos podemos encontrar nossa área de maneira simples fazendo
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = e - x ,y = x + 1ex = - 1
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = sen 2 x ,y = x + 2 ,x = 0ex = π / 2
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = 2 x , y = 2 - xey = 4
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = arcsen x , y = π 2ex = 0
Calcular a área da região limitada pelas seguintes curvas, dadas na forma paramétrica. x = cos t y = s e nt e x = cos t y = 1 2 s e nt