Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.3 - Ex. 58
Rota de um esquiador aquático – Suponha que um barco tenha sido posicionado na origem com um esquiador amarrado no ponto (30,0), como uma corda de 30 pés de comprimento. À medida que o barco viaja ao longo do eixo das ordenadas positivo, o esquiador é puxado pelo barco ao longo de um caminho desconhecido como mostra a figura a seguir:
- Mostre que
- Resolva a equação do item a para usando
Passo 1
- Galera, é o seguinte, temos um problema e para resolver precisamos observar a imagem dada na questão:
- Temos a . Então para encontrar a vamos integrar a
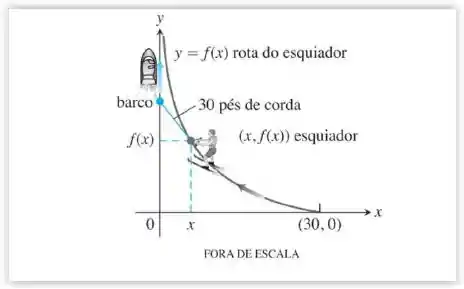
A inclinação da linha tangente a é dada por. Vamos considerar o triângulo cuja a hipotenusa é a corda de 30 pés. A base desse triângulo corresponde a medida e encontraremos a altura usando o Teorema de Pitágoras:
Chamaremos:
Hipotenusa
Cateto 1:
Cateto 2:
Assim, teremos:
Temos que a altura é
A inclinação da reta tangente é dada por que é a variação no eixo x sobre a variação no eixo y, o gráfico nos mostra uma função decrescente e portanto essa variação é negativa. Portanto:
Passo 2
Estamos diante de um caso de substituição trigonométrica, do tipo . Assim vamos considerar:
E agora, substituímos na integral:
Passo 2
Queremos a , então onde tiver colocaremos 30 e substituímos por 0: