Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 50

f x = ln ⁡ x - 1 - 1

  1. Quais são o domínio e a imagem de f ?
  2. Qual é a intersecção com o eixo x do gráfico de f ?
  3. Esboce o gráfico de f

Passo 1

Eaee, belezinha?? Bom... a questão nos dá a seguinte função:

f x = ln ⁡ x - 1 - 1

Sabendo disso, a questão nos faz três perguntinhas:

  1. Quais são o domínio e a imagem de f ?

    2. Lembrando que:

    Domínio: O conjunto de todos os valores para os quais a função está definida (aqui a gente vê se a função tem alguma restrição que faça com que ela deixe de ser real).

    Imagem: O conjunto de todos os valores que a função pode assumir como resultado.

  2. Qual é a intersecção com o eixo x do gráfico de f ?

    3. Quando f intercepta com o eixo x , temos que y = 0 .

  3. Esboce o gráfico de f .

Então bora junto!! 😉

Passo 2

Seguinte.. na letra a) a questão pede o domínio e a imagem da função.

A nossa função é:

f x = ln ⁡ x - 1 - 1

A única restrição que pode aparecer é no ln, né? Lembrando que o que estã dentro do ln não pode ser negativo e nem igual a zero, então temps:

x - 1 > 0

x > 1

O domínio é dado por D = x ∈ I R     x > 1 } = ( 1 , ∞ ) .

Imagem é dada por I M = R = ( - ∞ , ∞ ) .

Passo 3

Na letra b) a questão quer a intersecção com o eixo x do gráfico de f .

Com y = 0 , podemos escrever que:

0 = ln ⁡ x - 1 - 1

⇒ ln ⁡ ( x - 1 ) =   1  

Elevando ambos os lados da equação com a base e e utilizando a propriedade da função logaritmo natural:

e ln ⁡ x = x

Temos:

e ln ⁡ ( x - 1 ) = e 1

⇒ x - 1 = e 1

⇒ x = e + 1

Logo a função f intercepta o eixo x em x = e + 1 .

Passo 4

Por fim, na letra c) Para esboçar o gráfico podemos já marcar esse ponto onde a função intercepta o eixo x e depois esboçar a função.

Repara que a função é uma função logarítmica e tem um “ - 1 " depois do ln. Isso nos indica que a função está deslocada uma unidade para a direita.

E o ln, por mais que tenho o x - 1 dentro, a função vai continuar com aquela “carinha” de ln, mas mais achatada.

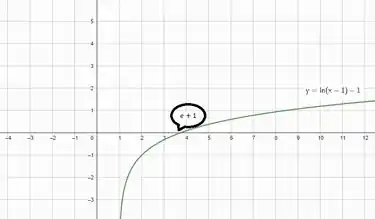
Esboçando o gráfico, temos:

Resposta

  1. D = x ∈ I R     x ≥ 1 } = ( 1 , ∞ ) e I M = I R = ( - ∞ , ∞ )
  2. f intercepta o eixo x em x = e + 1 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que o gráfico de y = log 2 ⁡ x seja feito sobre uma malha coordenada onde a unidade de comprimento seja 1 centímetro. Quantos quilômetros à direita da origem devemos percorrer antes de a altur
Resolva a inequação em x .1e^(3 x - 1)2
Resolva a inequação em x . 1 - 2 ln ⁡ x3
Resolva a inequação em x .ln x0