Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 49
- Quais são o domínio e a imagem de ?
- Qual é a intersecção com o eixo do gráfico de ?
- Esboce o gráfico de
Passo 1
Eaee, belezinha?? Bom... a questão nos dá a seguinte função:
Sabendo disso, a questão nos faz três perguntinhas:
- Quais são o domínio e a imagem de ?
- Qual é a intersecção com o eixo do gráfico de ?
- Esboce o gráfico de
A cada passo abaixo, a gente vai entendendo melhor o que cada letrinha pede, certinho??
Então bora junto!! 😉
Passo 2
Seguinte.. na letra a) a questão pede o domínio e a imagem da função.
Vamos entender cada um desses dois conceitos:
Domínio: O conjunto de todos os valores para os quais a função está definida (aqui a gente vê se a função tem alguma restrição que faça com que ela deixe de ser real).
Imagem: O conjunto de todos os valores que a função pode assumir como resultado.
O domínio é dado por , visto que não existe de número negativo.
E a imagem é dada por .
Passo 3
Na letra b) a questão quer a intersecção com o eixo do gráfico de .
Quando intercepta com o eixo , temos que .
Assim, podemos escrever que:
Elevando ambos os lados da equação com a base e utilizando a propriedade da função logartimo natural:
Temos:
Logo a função intercepta o eixo em .
Passo 4
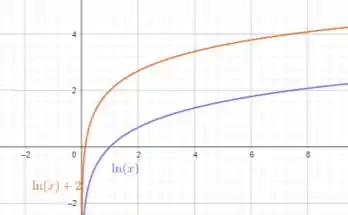
Por fim, na letra c), esboçando o gráfico de a partir de um gráfico conhecido, temos:
Note que pegamos uma função que temos conhecimento e deslocamos duas unidades para cima.
Resposta
- e ;
- intercepta o eixo em ;
