Quais são as projeções do ponto ( 2,3 , 5 ) nos planos x y , y z e x z ? Desenhe uma caixa retangular que tenha vértices opostos na origem e em ( 2,3 , 5 ) e suas faces paralelas aos planos coordenados. Nomeie todos os vértices da caixa. Determine o comprimento da diagonal dessa caixa.

( 2,3 , 0 ) ( 0,3 , 5 ) ( 2,0 , 5 ) 38u . m

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.1 - Ex. 4

Quais são as projeções do ponto nos planos e ? Desenhe uma caixa retangular que tenha vértices opostos na origem e em e suas faces paralelas aos planos coordenados. Nomeie todos os vértices da caixa. Determine o comprimento da diagonal dessa caixa.

Passo 1

Um ponto pertencente ao plano tem coordenadas , um ponto no plano tem coordenadas e um ponto em tem coordenadas , então para encontrarmos a projeção de em cada um desses planos, basta zerarmos a coordenada correspondente daquele plano. Assim:

Projeção de no plano é o ponto

Passo 2

Desenhando a caixa descrita, ficamos com:

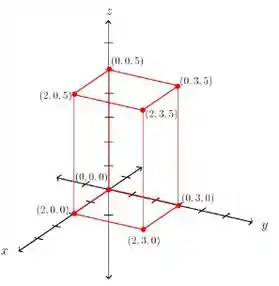
Passo 3

Agora queremos calcular o tamanho da diagonal azul desenhada:

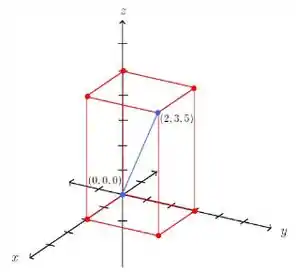
Para fazer isso, podemos calcular a distância entre os pontos e :

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam os pontos P (2,3) ,Q (4,2) e R (3,5) .Determinar vec u + vec v + vec w .

Sejam os pontos P 2,3 ,Q 4,2 e R 3,5 .Representar em um mesmo gráfico os vetores posição de u → , v → e w → de modo que Q = P + u → , R = Q + v → e P = R + w → ;

Dados os vetores vec u = (1 , - 1) , vec v = (- 3,4) e vec w = (8 , - 6) , calcular:|vec w|

Dados os vetores vec u = (1 , - 1) , vec v = (- 3,4) e vec w = (8 , - 6) , calcular:|vec u|

Dados os vetores vec u = (1 , - 1) , vec v = (- 3,4) e vec w = (8 , - 6) , calcular:|2 vec u - vec w|