Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 52
Um satélite de observação terrestre tem sensores de horizonte que podem medir o ângulo mostrado na figura abaixo. Seja o raio da Terra (supostamente esférica) e a distância entre o satélite e a superfície da Terra.
- Mostre que
- Obtenha até o grau mais próximo para um satélite que está a da superfície (use .
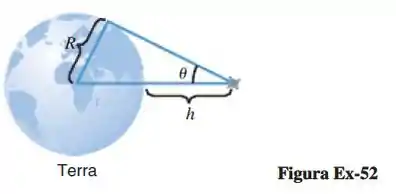
Passo 1
Olá povo bonito? Como vocês estão? Aqui ta tudo certinho :D. A primeiríssima coisa que nossa questão pede é provar que:
Onde é o raio da terra supostamente (hahaha) esférica
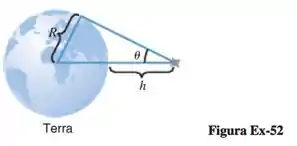
Ok ok, brincadeiras à parte, vamos ter também que é a distância entre o satélite e a terra. A figura do enunciado é essa:
Mas podemos, pra ficar mais claro, redesenhar esse triângulo retângulo para:
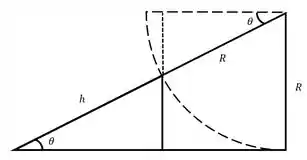
Po galera, olhando pra essa imagem, vemos que o triângulo maior que, mesmo a gente desconhecendo a base, conhecemos a altura “” e hipotenusa “”. E quem é que relaciona essas duas grandezas se não o seno? Sendo assim:
Passo 2
Pra fecharmos, a questão pede pra acharmos até o grau mais próximo para um satélite que está a da superfície, usando . Po galera, ta tudo na mesma unidade de medida, então nem preciso me preocupar com isso! Seja:
Usando esses valores de e numa ferramenta famosa de planilhas e a função =”ASEN()”, achamos o seguinte valor de :
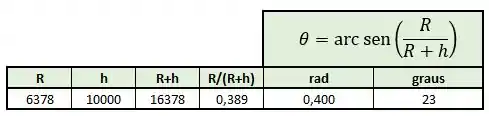
Logo:
Resposta
- Provado no Passo