Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 10
Encontre a fórmula para
Passo 1
Toda vez que formos inverter uma função galera, vamos seguir três passos, ok? São eles:
Por extenso, temos:
- Passo 1: Escrever a função como igual a uma função de
- Passo 2: Isolar de forma que possamos escrever ele como uma função de
- Passo : Trocar de lugar e chamar a nova função de encontrada da inversa
Bora lá?
Passo 2
Seja:
Se a gente somar e subtrair no numerador ao mesmo tempo, não mudamos nada, pois é como se tivéssemos adicionando zero! Olha a malandragem então:
Subtraindo dos dois lados, temos:
Multiplicando os dois lados por , temos:
Dividindo os dois lados por , temos:
Somando nos dois lados, temos:
Trocando de lugar:
Nossa inversa será então:
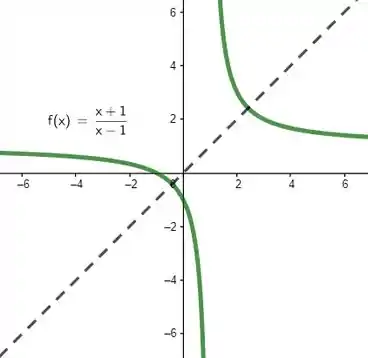
E gente olha que doido! A inversa é igual a função original! Isso acontece porque a função original já era simétrica em relação a mesmo, então a sua inversa acaba ficando igual. Ó só o gráfico que bonito:
Resposta
Exercícios de Livros Relacionados
Dado que y = t g - 1 ( - 2 ) , ache o valor exato de cada uma das funções:11. b) c o s( y )
Mostre que: cosh (ln (x)) = (x^2 + 1)/(2 x)
Num circuito elétrico, a força eletromotriz é x volts em t s, onde E = 20 cos 120 π t . (a) Resolva a equação em t . Use a equação da parte a) para achar o menor valor positivo de t para o qual a fo
Nos exercícios de 34 a 41, faça um esboço do gráfico da curva com a equação dada.36. y = ln ( x + 1 )
Faça um esboço do gráfico de y=l nx , colocando no gráfico os pontos com abcissas 1/9, 1/3, 1 ,3 e 9 e use l n3= 1,1 . Em cada um dos cinco pontos, ache a inclinação da reta tangente e trace um segmen