Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 42
- Use um recurso gráfico computacional ajustado para medir radianos para fazer tabelas dos valores de e com Arredonde suas respostas para duas casas decimais.
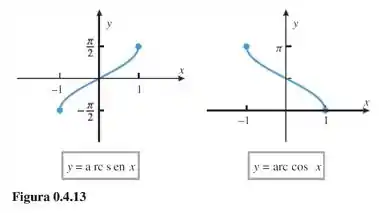
- Plote os pontos obtidos em e use-os para esboçar os gráficos de e . Confirme que seus esboços estão de acordo com aqueles da Figura .
- Use seu recurso computacional para fazer o gráfico e confirme que seus esboços estão de acordo com aqueles da Figura .
Passo 1
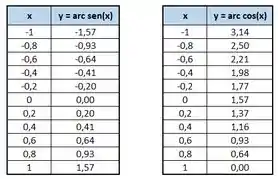
Galera, nessa questão aqui vamos precisar usar o computador!. Usando uma ferramenta famosíssima de planilhas, dá pra resolver tudo. A função ASEN já é ajustada pra radianos, e o arredondamento já acontece automaticamente pra quantidade de casas desejadas quando escolhemos quantas exibir! Sendo assim, esse recurso vai nos retornar esses valores pra :
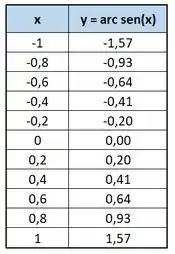
E pra :
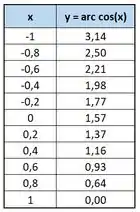
Passo 2
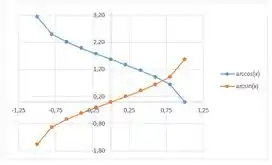
Agora é a parte que eu mais gosto hahaha gráficos! Aqui vamos usar os pontos que conseguimos pra marcar esses pontos. Podemos usar a mesma ferramenta de planilhas, já que ela possui ferramentas gráficas de dispersão. A questão pede pra gente marcar os pontos e depois usar eles pra esboçar o gráfico. Então o que faremos é programar a dispersão pra conectar os pontos, ok? Selecionando adequadamente a coluna dos valores de e de , obtemos, para :
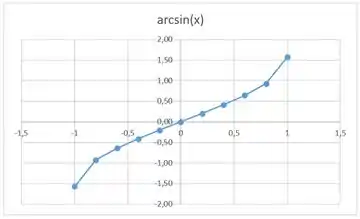
E pra :
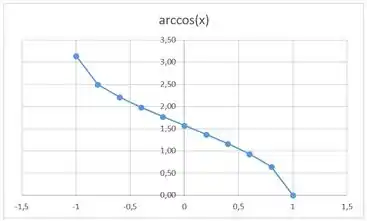
Comparando esse resultado com a Figura ., imediatamente abaixo, vemos que tá bem parecidinho, então fizemos as contas certo e obtivemos um esboço bom das funções e :
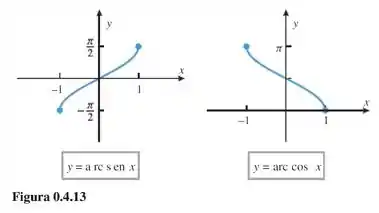
Olha, normalmente faltaria ainda a letra , mas na verdade a é no papel e a é no computador hahaha como eu e você estamos conversando pelo computador mesmo, pra cá a ficam a mesma coisa, ok? Mas tenta fazer no papel também e vê se fica parecido! Bora pra próxima questão!
Resposta
- Fazer no Papel
