Uma escada com de comprimento está apoiada em uma parede vertical. Seja o ângulo entre o topo da escada e a parede, e a distância da base da escada até a parede. Se a base da escada escorregar para longe da parede, com que rapidez variará em relação a quando ?
Passo 1
Eaee, belezinha?? Bom... uma escada com de comprimento está apoiada em uma parede vertical da seguinte forma:
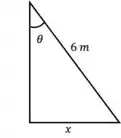
Queremos descobrir a rapized que irá variar em relação a quando
Bom... como o problema está pedindo a rapidez com que varia, ou seja, sua derivada, então temos que relacionar primeiramente e .
Depois é só aplicar a derivada e substituir !!
Bora lá!! 😉
Passo 2
Bom... pela figura podemos perceber que a relação entre e é:
Agora já podemos derivar!!
Lembrando que a derivada do seno é:
Passo 3
Derivando em função de temos:
Quando :
Assim, estará variando em relação a a uma taxa de .
Entendeu direitinho?? Responde aee 😉
Resposta
estará variando a uma taxa de .