Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.Exercícios Práticos - Ex. 39
Seja.
- Utilize o teorema do valor intermediário para mostrar que possui um zero entre e .
- Resolva a equação graficamente com um erro de magnitude de no máximo
- Pode-se mostrar que o valor exato da solução no item (b) é
Passo 1
Resolvendo o item (a):
Primeiramente, precisamos estudar a continuidade da função .
Devemos notar que por ser formada por um único polinômio, o seu domínio é o conjunto e não há restrição alguma para a existência de limites. Logo, concluímos que a função é contínua no intervalo
Passo 2
Sabendo que a função é contínua, calculamos agora os valores e
Passo 3
Sabendo que e que ,
Podemos afirmar, pelo teorema do valor intermediário, que, como a função é continua em , existe um , tal que .
Portanto, como , possui um zero entre e .
Passo 4
Resolvendo o item (b):
Obtendo duas funções: e
Podemos observar o gráfico das duas curvas
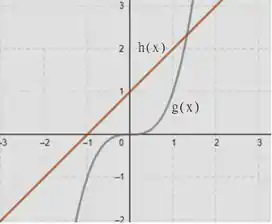
Aproximando o gráfico, podemos analisar melhor o ponto de encontro das curvas.
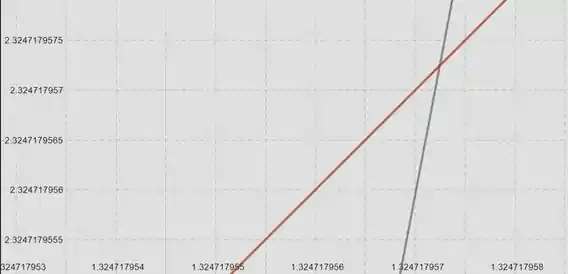
O valor de que procuramos é o valor da abscissa na interseção das curvas. Logo, considerando um erro de magnitude , o valor de para está entre 1,3247179570 e 1,324719575
Passo 5
Utilizando uma calculadora científica para resolver a seguinte expressão
Encontramos o valor 1,3247195724. Logo, o resultado observado graficamente está dentro da margem de erro.
Resposta
Ei, a resposta está no passo a passo :)