Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 10

Seja F x , y = 1 + 4 - y 2 .

  1. Calcule F ( 3,1 ) .
  2. Determine e esboce o domínio de F .
  3. Determine a imagem de F .

Passo 1

Falaaa aí! Tudo joinha?

O objetivo da questão é calcular o valor da função F x , y = 1 + 4 - y 2 . para valores específicos de x e y .

Vamos matar mais essa?

  1. Na letra A, temos que encontrar o valor específico da função quando x = 3 e y = 1 .
  2. Na letra B, temos que determinar e esboçar o domínio de F , identificando os valores de x e y para os quais a função está definida.
  3. Na letra C, vamos determinar a imagem de F . Encontrando todos os valores possíveis que a função posso assumir ao variar x e y dentro do domínio.

E como podemos resolver isso? Se liga!

  1. Vamos iniciar com a letra A, substituindo os valores dados de x e y na expressão da função e simplificar para obter o resultado numérico.
  2. Para determinar o domínio de F na letra B, vamos identificar as restrições da função, que nesse caso, lembrando que o radicando deve ser maior ou igual a zero. Ao resolver a inequação obtemos o intervalo que mantém a função definida.
  3. E para finalizar, a letra C. Para encontrar os valores mínimos e máximos, e para isso temos que usar a função 4 - y 2 .

Passo 2

a) A gente quer calcular F ( 3,1 ) . Isso significa que a gente vai substituir x = 3 e y = 1 na nossa função F ( x , y ) , beleza? Vamos lá!

Nossa função é: F x , y = 1 + 4 - y 2 . Maaaas... não tem x nela!! Onde que a gente vai substituir x = 3 ?

Bom, a gente não vai! Se não tem o x ali, não se preocupe com ele. Vamos substituir só o y ...

F 3,1 = 1 + 4 - 1 2

F ( 3,1 ) = 1 + 3

Prontinho! Essa já foi!

Passo 3

Agora vamos pro domínio!

Letra B - Vamos escrever nossa função assim:

z = 1 + 4 - y 2

Qual restrição a gente tem aqui?

A raiz quadrada não pode ser negativa, não é?

Ou seja, a gente precisa que:

4 - y 2 ≥ 0

- y 2 ≥ - 4

y 2 ≤ 4

Temos então

y ≥ - 2     e   y ≤ 2

Como o x   não tá na função, ele pode assumir qualquer valor.

O domínio então é:

D = x , y 4 - y 2 ≥ 0 } → { ( x , y ) | x ∈ R ,   y ∈ - 2,2 }

Passo 4

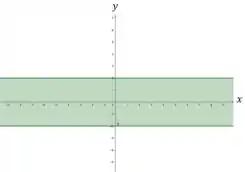
O domínio da função F é D = x , y x ∈ R ,   - 2 ≤ y ≤ 2 } .

Temos então uma faixa horizontal no plano x y onde y varia de - 2 a 2 e x pode ser qualquer valor real.

Passo 5

Vamos ver a imagem agora.

Bom, pensa só: a raiz é sempre positiva, certo? Então:

4 - y 2 ≥ 0

Veja também que o valor máximo pra essa raiz é quando y = 0 , ou seja:

4 - 0 2 = 4 = 2 é o máximo que essa raiz pode atingir (porque o y 2 tá negativo, então qualquer valor aí vai diminuir a raiz)

Ou seja, a gente tem:

0 ≤ 4 - y 2 ≤ 2

Então se a gente somar 1 em todos os pedacinhos:

1 ≤ 1 + 4 - y 2 ≤ 3

E aí chegamos na nossa função, então a imagem é:

[ 1,3 ]

E encerramos por aqui nossa questão😉

Resposta

  1. F 3,1 = 1 + 3
  2. D = x , y 4 - y 2 ≥ 0 } → { ( x , y ) | x ∈ R ,   y ∈ - 2,2 }
  3. I m F = [ 1,3 ]
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja F um subconjunto do I R 2 . Dizemos que F é um conjunto fechado se o conjunto de todos os ( x , y ) não-pertencentes a F for aberto. Verifique quais dos conjuntos a seguir são fechados.d) x , y ∈
Seja F um subconjunto do I R 2 . Dizemos que F é um conjunto fechado se o conjunto de todos os ( x , y ) não-pertencentes a F for aberto. Verifique quais dos conjuntos a seguir são fechados.g) x , y ∈
Seja F um subconjunto do I R 2 . Dizemos que F é um conjunto fechado se o conjunto de todos os ( x , y ) não-pertencentes a F for aberto. Verifique quais dos conjuntos a seguir são fechados.c) x , y ∈
Desenhe a imagem:3. F (t) = (2 t - 1 , t + 2)
Desenhe a imagem:6. F (t) = ( t^2 , t^4 )