Seja f x = x , x ∈ 0,1 . Considere a sequência de termo geral S n = f 1 n 1 n + f 2 n 1 n + f 3 n 1 n + … + f n - 1 n 1 n + f 1 1 n. a) Calcule S 3 . Observe que, geometricamente, S 3 pode se interpretado como a soma das áreas dos retângulos hachurados.b) Calcule lim n → + ∞ ⁡ S n (Pensando geometricamente, qual o valor esperado para o limite?)

a) S 3 = 2 3 b) lim n → + ∞ ⁡ S n = 1 2

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.3 - Ex. 4

Seja , . Considere a sequência de termo geral

a) Calcule . Observe que, geometricamente, pode se interpretado como a soma das áreas dos retângulos hachurados.

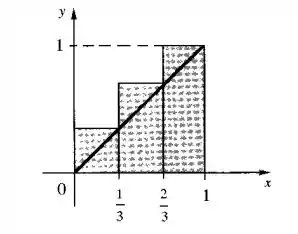
b) Calcule (Pensando geometricamente, qual o valor esperado para o limite?)

Passo 1

a) Temos que é dado por:

Passo 2

b) Podemos ver que corresponde também, ao número retângulos, os quais a sua extremidade superior direita se alinha à função, fazendo com que a altura dos retângulos seja o valor da função. E nos dá a soma dessas áreas.

Quando o número de retângulos converge para o infinito, os retângulos estarão todos alinhados com a região abaixo da curva de , ou seja, a soma das áreas dos retângulos converge para a área do triângulo delimitado pela figura.

Como a área do triângulo é:

Logo:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se a sequência converge ou diverge. Se convergir, encontre o limite. a n = cos 2 ⁡ n 2 n

Determine se a sequência converge ou diverge. Se convergir, encontre o limite. a n = ln ⁡ n + 1 - ln ⁡ n

Determine se a sequência converge ou diverge. Se convergir, encontre o limite. a n = a r c t a n ⁡ ( ln ⁡ n )

Determine se a sequência converge ou diverge. Se convergir, encontre o limite. a n = n n

Determine se a sequência converge ou diverge. Se convergir, encontre o limite. a n = 2 - n c o s n π