Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.3 - Ex. 58
Seja .
- Faça o gráfico de f. Que tipo de descontinuidade parece ocorrer em 0?
- Calcule os limites laterais de f em 0. Esses valores confirmam sua resposta para a parte?
Passo 1
Olá, amigo, Yuri aqui e irei estar te ajudando a resolver essa atividade de limite.
A questão nos pede para primeiro construir o gráfico da função dada, e por um spoiler do enunciado analisar qual a descontinuidade existe nesta função.
Existem alguns tipos de descontinuidade, são eles:
Descontinuidade removível: A função tem uma descontinuidade removível quando os valores calculados em e são diferentes. Assim observamos que um ponto da função é “deslocado” ou deixa de existir
Descontinuidade de salto: Na descontinuidade de salto observamos que os limites laterais são diferentes, por isso dizemos que a função “deu um salto” em um determinado valor de x.
Descontinuidade essencial: As funções que possuem descontinuidade essencial são as que possuem assíntotas verticais, ou seja, aquelas nas quais obtemos ao calcularmos os limites laterais.
Passo 2
Letra a)
O gráfico da função é dado abaixo, ele foi construído utilizando o GeoGebra.
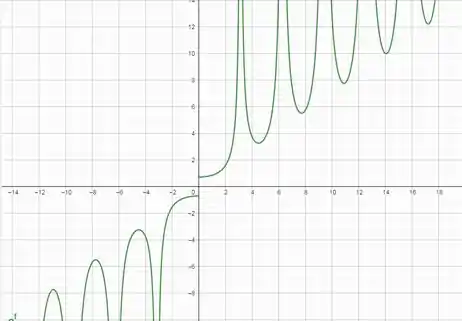
A descontinuidade está presente quando nos aproximamos a , ali vemos que os valores da função são diferentes a depender por qual direção de tomamos. Temos então uma descontinuidade de ‘salto’, pois temos um ‘salto’ no valor da função a depender de qual lado nos aproximemos.
Passo 3
Letra b)
Queremos os limites laterais, ou seja, quando tende a zero pela direita e pela esquerda.
Depois de calcularmos esses limites iremos analisar se o resultado faz jus ao gráfico que montamos na letra A.
Primeiro iremos modificar o termo utilizando de transformações trigonométricas.
Sabendo que podemos reescrever:
Ao retirar a raiz, precisamos colocar em modulo:
O limite pela esquerda em :
E por que é negativo? Pois
e por conta do modulo devemos colocar o sinal negativo.
Continuando nossos cálculos:
Tiramos primeiro a constante do limite, após isso utilizamos uma manipulação matemática para termos dentro do nosso limite o termo:
pois sabemos previamente que
Então temos,
O limite da divisão é igual a divisão de limites:
Finalmente calculando o limite:
Passo 4
Agora iremos trabalhar com o limite pela direita:
O sinal é positivo aqui pois , e não existe mais a necessidade de se colocar o sinal negativo.
Veja que aqui utilizamos das mesmas manipulações que utilizamos no limite pela esquerda.
O limite da divisão é igual a divisão de limites:
Como os limites à esquerda e à direita são diferentes, há uma descontinuidade por salto em . Isso confirma a solução da parte (a).
Resposta
- Descontinuidade por salto