Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.2 - Ex. 74
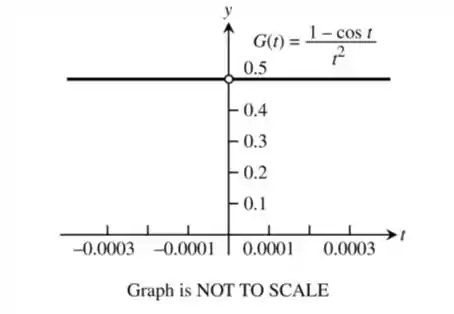
74. Seja .
a. Faça uma tabela dos valores de em valores de que se aproximam de por cima e por baixo. Em seguida, estime
b. Apoie suas conclusões no item (a) ao fazer o gráfico de próximo a .
Passo 1
a.
Para fazermos essa tabela, só precisamos ir jogando os valores, cada vez mais próximos de , na fórmula e ver para onde está tendendo:
Podemos observar que está se aproximando de
tanto por cima quanto por baixo.
Passo 2
b.
Podemos fazer um esboço do gráfico plotando os pontos calculados em (a). Para a função não está definida, mas ela possui um limite nesse ponto, que foi calculado em (a) e que podemos usar para construir o gráfico.
O gráfico dessa função vai ficar assim:
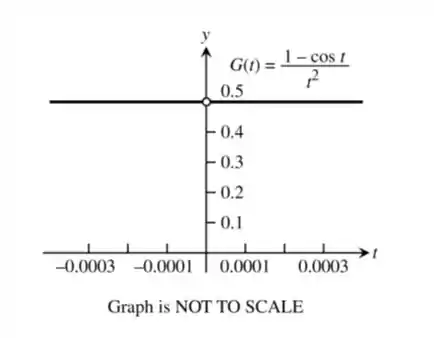
Resposta
a.
b.
Exercícios de Livros Relacionados
60- Mostrando que L não é um limite Podemos provar que lim x → x 0 f ( x ) ≠ L ao fornecer um ϵ0 de modo que não seja possível encontrar δ0 que satisfaça a condição.Para todo x , 0x - x 0δ → f x - L
57- Mostrando que L não é um limite Podemos provar que lim x → x 0 f ( x ) ≠ L ao fornecer um ϵ0 de modo que não seja possível encontrar δ0 que satisfaça a condição.Para todo x , 0x - x 0δ → f x - L
58- Mostrando que L não é um limite Podemos provar que lim x → x 0 f ( x ) ≠ L ao fornecer um ϵ0 de modo que não seja possível encontrar δ0 que satisfaça a condição.Para todo x , 0x - x 0δ → f x - L
8-Faça o gráfico de Determine lim x → 1 + f ( x ) e lim x → 1 - f ( x ) .Existe lim x → 1 f ( x ) ? Em caso afirmativo, qual é? Em caso negativo, por que não?
10- Faça os gráficos das funções nos Exercícios 9 e 10. Em seguida, responda às questões.Qual é o domínio e a imagem de f ?Em que pontos c , se houver, lim x → c f ( x ) existe?Em que pontos existe