Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.3 - Ex. 57
57- Mostrando que L não é um limite Podemos provar que ao fornecer um de modo que não seja possível encontrar que satisfaça a condição.
Para todo , .
Conseguimos isso para o nosso candidato ao mostrar que para cada existe um valor de tal que
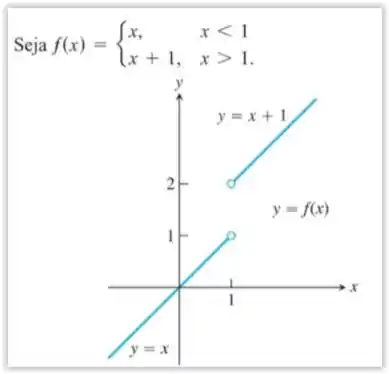
- Seja . Mostre que nenhum satisfaz a seguinte condição :
- Mostre que
- Mostre que
Para todo , . Isto é, para cada ,mostre que há um valor de tal que
Isso mostrará que
Passo 1
Na letra a essa proposição nos satisfará pois pegaremos um quadrado de amostra de tamanho em para a reta , pois essa função não tem limite de para esse valor.
E como foi estipulado naturalmente escolheríamos valores de iguais a e . Só que na função limitada de não existe valor possível para a função, não havendo consequentemente um positivo. Logo:
Nos daria:
Assim como:
Sendo impossível ser igual 2 não importando qual seja o valor de
Qualquer valor da reta com o domínio dará um valor maior que
Passo 2
Na letra b devemos provar que vindo da direita a função não tenha limite igual a 1, pois a esquerda ela já possui.
Logo
Só que naturalmente essa função nos faz observar valores de iguais a e porém como nosso domínio é restringido em então não teremos valor negativo de consequentemente. Fazendo com que:
O que é:
Só que nossa função é vemos:
Então nunca teremos um valor de limite igual a 1 para essa função.
Em outras palavras vimos que .
Como o menor valor de será 1 teremos:
Passo 3
Como a primeira equação nos dá
E a segunda :
Logo nunca teremos um limite que vindo de nenhum dos lados que dê 1.5.
Pegando como exemplo a função
O que é:
Como o menor valor de nessa função é 1 logo:
O que prova
Resposta
Ei, a resposta está no passo a passo :)