Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 8.2 - Ex. 8
Seja Desenhe a imagem da curva , onde e (R>0) . Como é o gráfico de ?
Passo 1
Vamos tentar desenhra primeiro a curvaa , beleza?
Perceba que ela já parecer com uma curva que conhecemos(, então, isso nos dá mais ou menos a ideia do que poderá ser. Nossa curva a ser desenhada é
Sacou por q?
Quando substituimos os valores de dependendo de , nossa função tem a cara
.
Perceba que nossa curva vai ser fechada, por conta das coordenadas e . E que o é quem determina abertura da curva ( se vai ser mais fechadinha, abertinha).
Vamos desenhar, então.
Passo 2
Para desenhar a curva, precisamos do auxílio de um software. Mas, dá pra ter uma ideia do que vai aparecer, se olharmos para as curvas de nível, temos que próximo a origem temos parábolas.
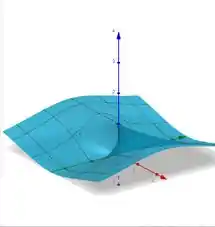
Resposta
Ei, a resposta está no passo a passo :)