Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.4 - Ex. 10
Seja . Determine a reta contida no gráfico de , passando pelo ponto e que forma com o plano ângulo máximo.
Passo 1
Show galera, bora começar. Pra início de conversa, como queremos uma reta contida no plano:
Que também passa pelo ponto , de forma geral, podemos dizer que essa reta terá o formato:
Onde é o vetor director dessa reta, que é a única coisa que precisamos achar mesmo! Bora lá então.
Passo 2
Acredita em mim quando eu digo: dois pontos definem uma reta. Logo pra saber o vetor diretor, basta eu encontrar dois pontos. Um deles deve ser exatamente o ponto :
Já que nossa reta tem que passar por aí mesmo. O truque tá no outro ponto, que pra gente ver o ângulo com o plano , tem que ser um ponto pertencente a esse plano. Show de bola! Veja o seguinte, quando , obtemos:
Logo:
Sendo assim, o conjunto de pontos que fazem parte do plano e do plano ao mesmo tempo pode ser descrito como:
Oras, então já que tanto quanto são pontos pertencentes ao plano , o vetor também será! E será também nosso vetor diretor da reta! Calculando:
Em grafiquês, temos isso:
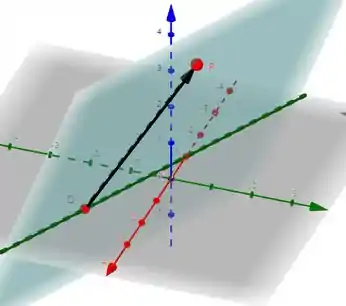
Onde o plano está em azul e o ponto é móvel, dependendo do valor de , podendo se mover ao longo da linha tracejada verde. Falta a gente achar o valor do parâmetro que maximize o ângulo com o plano .
Passo 3
Pra gente achar esse ângulo, vamos montar um segundo vetor: um vetor pertencente ao plano que é a projeção de nesse plano. Seja o ponto a projeção de no plano , esse vetor que queremos será na verdade:
O que em grafiquês é:
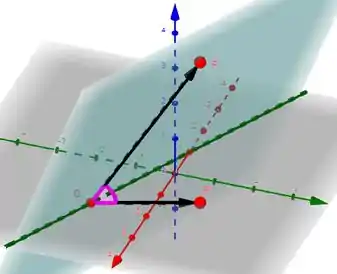
E o ângulo que o vetor diretor faz com o plano nada mais é do que esse carinha rosa marcado acima. Pra maximizar esse ângulo, podemos construir uma função de ! Pra isso, podemos lembrar do produto escalar entre vetores:
Fazendo isso, temos:
Eita, ficou enorme né? Mas calma, nota o seguinte, tudo ai é muito parecido. Chamando:
Vamos ter:
Otimizando então, devemos derivar e igualar a zero, então:
O que resulta em:
Como
Vemos que é impossível, já que é uma soma de termos ao quadrado. Fechamos então com a condição:
Passo 4
Achamos então como um ponto crítico de . Já adianto que se testarmos, veremos que esse é um ponto de mínimo para , o que é exatamente o que queremos, uma vez que o ângulo aumenta conforme diminuí! Logo o ponto de mínimo para é de máximo para ! Sendo o vetor diretor:
O ângulo máximo ocorre quando:
Pra não deixar feio, e só ficar com números inteiros aí, podemos multiplicar por e dividir por e achar um vetor com mesma direção e sentido que o acima:
A reta será: