Suponha que represente uma distribuição de temperatura no plano xy, (Admita que x e y sejam dados em km e a temperatura em ᵒC.) Um indivíduo encontra-se na posição (3,2) e pretende dar um passeio.
A) Descreva o lugar geométrico dos pontos que ele deverá percorrer se for o seu desejo desfrutar sempre da mesma temperatura do ponto (3,2).
B) Qual a direção e sentido que deverá tomar se for seu desejo caminhar na direção de maior crescimento da temperatura?
C) De quanto a temperatura se elevará aproximadamente, caso caminhe 0,01 km na direção encontrada no item B?
D) de quanto decrescerá, aproximadamente, a temperatura, caso caminhe 0,01 km na direção ?
Passo 1
STAND BY ME, OH, STAND BY...Opa, não vi você chegando, voltou para mais uma questão né? Eu conheço muito bem esse tipo de olhar, então, veio ao lugar certo, essa não é difícil, não deixa o tamanho dela te intimidar, na questão é dado o ponto inicial do carinha e a equação da temperatura nesse plano, iremos usar essas informações, mas primeiro vou começar apresentando as equações que usaremos, simbora.
(1)
(2)
UÉ, MAS SÓ ISSO? Sim, usaremos apenas duas equações, agora que aquele pequeno susto inicial foi embora, vamos resolver mais essa.
Passo 2
Vamos começar pela letra A.
Começaremos pegando a temperatura do ponto A, para isso, é só substituir na equação dada pela questão:
ᵒC
Agora que temos a temperatura desejada, basta implementá-la na equação anterior, vai ficar assim ,meu bom:
E com isso, chegamos à conclusão que a forma geométrica na qual todos os pontos possuem essa temperatura de ᵒC é uma elipse, vamos seguir para a...O que? Você não sabe de onde tiramos que isso é uma elipse? OH CÉUS, pequeno gafanhoto, vai ver uma aula sobre Cônicas, é de Geometria Analítica, o Responde aí tem esse tipo de conteúdo, certeza, vai lá, depois volta aqui, enfim, continuando, vamos seguira para a letra B, mas antes, toma a selfie que essa elipse me mandou:
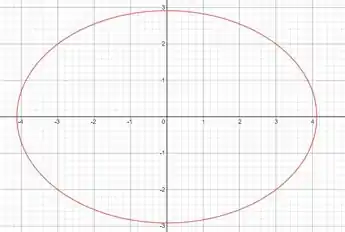
Passo 3
Vamos ver essa letra B....agora sim, como ele quer caminhar na direção onde ocorre maior crescimento de temperatura, então, usaremos o vetor gradiente para saber em que direção e sentido ele deve ir:
PRONTINHO, Agora sabemos que a partir do ponto A (3,2), a direção que se obtém o maior incremento na temperatura é a mesma do vetor gradiente: , ou seja, se quiser ir na direção de onde fica mais quente, SEGUE O GRADIENTE, até rimou rs.
Passo 4
Simbora nessa letra C, aqui teremos que usar a derivada direcional:
Como buscamos uma taxa máxima de variação, podemos dizer que:
Com isso...oi meu anjo? Oh céus, não sabe o porquê disso? Corre aí no Responde Aí e vai ver umas aulinhas sobre gradiente e derivada direcional...continuando...com isso, teremos a taxa de crescimento máxima, então, vamos ver no que vai dar.
Ou seja, tratando as coordenadas dos pontos como quilômetros andados, e sabendo que a derivada direcional é relacionada a direção de um vetor unitário, podemos dizer que, a cada 1km andado aumenta-se , então se andarmos 0,01 km na direção do gradiente, teremos um crescimento máximo proporcional aos 0,01 km andados , ou seja, a temperatura aumentará , PRONTINHO, menos uma alternativa, estamos chegando perto de resolver essa aqui, ajeita essa postura e vamos juntos!
Passo 5
BORA NESSA LETRA D, para finalizar, tava vendo aqui, ela fala sobre decrescimento, então, é só colocar um sinal negativo no gradiente para termos a direção do decrescimento:
-
-
Agora, precisamos da derivada direcional para saber o que acontece quando o carinha anda 0,01 km na direção de , usaremos o na derivada direcional, já que é um vetor unitário e estaremos calculando a variação em relação a ele:
Agora sabemos que a temperatura decresce em 1km andado na direção do vetor j, logo, ela decrescerá 0,08 quando o individuo andar 0,01 km na direção de j.
RESOLVEMOS TUDO, agora eu quero relaxar, mas em que sentido? Falou galera, bons estudos, essa questão foi um pouco extensa, mas nada muito desafiador, então não se assuste com o tamanho, até a próxima ;)
Resposta
A) (elipse)
B)
C)
D)