Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.8 - Ex. 10
Seja .
- Encontre a equação da reta secante que passa pelos pontos e .
- Mostre que há somente um número no intervalo que satisfaz a conclusão do Teorema do Valor Médio para a reta secante em (a).
- Encontre a equação da reta tangente ao gráfico de no ponto .
- Use um recurso gráfico computacional para gerar a reta secante de (a) e a tangente de (c) no mesmo sistema de coordenadas e confirme visualmente que as duas são paralelas.
Passo 1
(a) A gente pode lembrar que a equação da reta pode ser dada por:
Sendo que . Então só precisamos calcular , e substituir na equação da reta, belezinha?
Passo 2
Vamos escolher como nosso ponto , e o outro ponto como .
Precisamos encontrar os valores de e , usando a função do enunciado:
Agora podemos achar :
E, pela equação da reta:
Passo 3
(b) Esse é o Teorama do Valor Médio:
A gente só precisa confirmar se nossa função é contínua e diferenciável no intervalo para usar ele. Como ela é um polinômio, isso é verdade. Podemos seguir tranquilos!
O que o enunciado quer é que a gente monte essa equação e descubra que só existe um valor de , que vai solucionar ela dentro desse intervalo. Vamos lá!
Passo 4
Precisamos calcular a derivada da nosssa função para montarmos . Fica assim:
Para montar o outro lado da equação, vamos achar e , substituindo e na função que ele deu:
Passo 5
Com todas essas informações, podemos montar nossa equação:
Isolando :
Como estamos no intervalo (bolinha aberta em ):
Passo 6
(c)Lembrando que a equação da reta tangente é:
Precisamos encontrar e para .
Vamos calcular :
E . Substituindo na nossa equação da reta:
Passo 7
(d) Agora é só colocar as duas retas que a gente achou no mesmo gráfico:
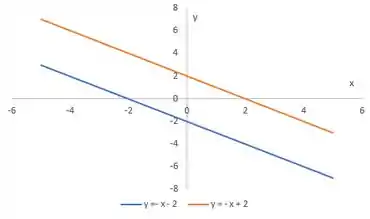
Resposta
(prova nos passos)
