a) Seja Encontre em x=1, sendo
b) Esboce o gráfico de mostrando dy e na figura.
Passo 1
a) Observe que:
Para temos:
Passo 2
Calculando agora o
Para temos:
Passo 3
Desenho:
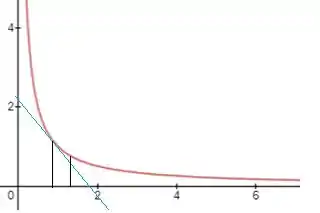
Resposta
Ei, a resposta está no passo a passo :)
a) Seja Encontre em x=1, sendo
b) Esboce o gráfico de mostrando dy e na figura.
a) Observe que:
Para temos:
Calculando agora o
Para temos:
Desenho:

Ei, a resposta está no passo a passo :)