Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.8 - Ex. 9g

Seja f x =   1 x                     ,             x < 0             x 2             ,     0 ≤ x < 1 2                 ,         x = 1 2 - x ,         x > 1

Esboce o gráfico e calcule o limite indicado se existir:

lim x → 2 - ⁡ f x

Passo 1

O gráfico da função f ( x ) é dado por:

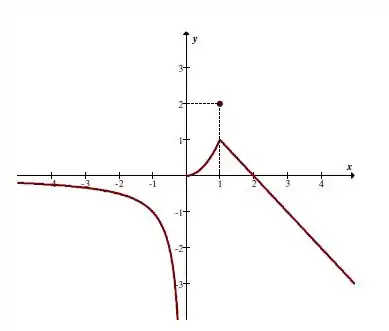
Passo 2

Para x > 1 ,   f x = 2 - x . Então, temos que:

li m x → 2 - f x = lim x → 2 -   ⁡ 2 - x

Passo 3

Aplicando o limite, temos que:

lim x → 2 - ⁡ 2 - x = 0

Resposta

0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja h x =| x | x , s ex ≠ 0 0 , x = 0 Mostrar que h ( x ) não tem limite no ponto 0 .
Seja f x =1 x , x0 x 2 , 0 ≤ x1 2 , x = 1 2 - x , x1 Esboce o gráfico e calcule o limite indicado se existir: lim x → 1 ⁡ f x
Seja g x =| x - 3 | x - 3 , x ≠ 3 0 , x = 3 Esboce o gráfico de g ( x ) .Achar, se existirem lim x → 3 + ⁡ g x , lim x → 3 - ⁡ g xe lim x → 3 ⁡ g ( x ) .
Esboçar o gráfico das seguintes funções e dar uma estimativa dos limites indicadosa) f x = x 2 - 9 x - 3 ;lim x → 3 ⁡ f x
Esboçar o gráfico das seguintes funções e dar uma estimativa dos limites indicadosd) f x = x - 1 x 3 - 1 ;lim x → 1 ⁡ f x