Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.8 - Ex. 9h

Seja f x =   1 x                     ,             x < 0             x 2             ,     0 ≤ x < 1 2                 ,         x = 1 2 - x ,         x > 1

Esboce o gráfico e calcule o limite indicado se existir:

lim x → 2   ⁡ f x

Passo 1

O gráfico da função f ( x ) é dado por:

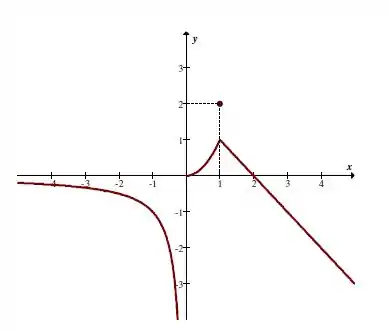
Passo 2

Dado que lim x → 2 - ⁡ 2 - x = 0       e lim x → 2 + ⁡ 2 - x = 0 , conclui-se que como os limites laterais são iguais, lim x → 2 ⁡ f ( x )   existe e é dado por:

lim x → 2 ⁡ f ( x ) = 0

Essa afirmação pode ser feita devido a definição do seguinte Teorema:

Se f é definida em um intervalo aberto contendo a exceto possivelmente no ponto a , então

lim x → a ⁡ f x = L     s e   e   s o m e n t e   s e   lim x → a + ⁡ f x = L   e   lim x → a - ⁡ f x = L .

Resposta

0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o limite. lim x → - 1 ⁡ x 3 + 1 x 2 - 1
Calcule o limite. lim t → - 2 ⁡ t 3 + 4 t 2 + 4 t t + 2 t - 3
Esboçar o gráfico das seguintes funções e dar uma estimativa dos limites indicadosb) f x = x 2 - 3 x + 2 x 2 - 4 ;lim x → - 2 ⁡ f x
Calcule o limite. lim t → 5 / 2 ⁡ 2 t 2 - 3 t - 5 2 t - 5
Esboçar o gráfico das seguintes funções e dar uma estimativa dos limites indicadosc) f x = x - 1 x 3 - 1 ;lim x → 1 ⁡ f x