Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 3.2 - Ex. 6c
6. Seja .
c) Esboce o gráfico de
Passo 1
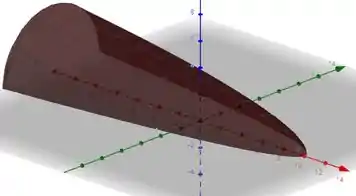
Esboçar o gráfico de nada mais é que desenhar a seguinte superfície:
Mas para as informações acima fazerem sentido, temos que considerar as seguintes condições: , que são condições que já observamos nos itens anteriores.
A equação nos descreve um parabolóide elíptico com o eixo geratriz coincidente com o eixo coordenado e com vértice . Além do vértice, temos que o parabolóide contém a parábola e a semi-circunferência , pois .
Sabendo isso, superfície será a seguinte(O eixo vermelho corresponde ao eixo , o eixo verde corresponde ao eixo e o azul é o eixo ):
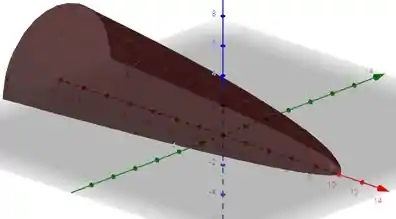
Resposta
Exercícios de Livros Relacionados
6. Seja f x , y = 10 - x - y 2 b) Identifique as interseções do gráfico de f com os planos z = 0 , z = 1 , z = 2 , y = 0 , e x = 0 .
4- Dada a função f x ,y = 1 x 2 + y 2 , pede-sec)Um esboço do gráfico da função.
6. Seja f x , y = 10 - x - y 2 a) Represente o domínio de f no plano x y e determine a imagem de f .
5-Considere a superfície z = f ( x ,y ) , onde: f x ,y = 8 - x 2 - y 2 , x 2 + y 2 ≤ 4 4 , x 2 + y 2 ≥ 4 Pede-se:a)As interseções da superfície com os planos z = 8 ,z = 6 ,z = 0 ,x = 0 e y = 0 .