6. Seja

b) Identifique as interseções do gráfico de com os planos , , , e

.

Para fazer a análise dessas interseções, basta substituir os valores dados na expressão da função

1)

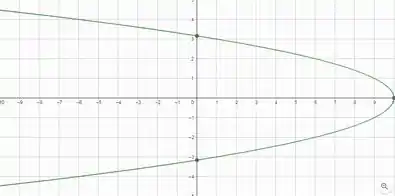
A partir daí, temos que a interseção do gráfico de com o plano é dada por

.O gráfico é dessa forma.

*Os gráficos de 2, 3 e 4 são muito parecidos, para os gráficos 1, 2 e 3 a diferença se encontra apenas no vértice e no plano . No gráfico 4, a parábola está no plano com

2)

A partir daí, temos que a interseção do gráfico de com o plano é dada por .

3)

A partir daí, temos que a interseção do gráfico de com o plano é dada por .

4)

A partir daí, temos que a interseção do gráfico de com o plano é dada por

.

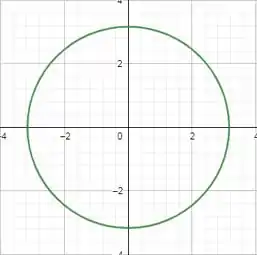
5)

A partir daí, temos que a interseção do gráfico de com o plano é dada por

.