6. Seja

a) Represente o domínio de no plano e determine a imagem de .

a) Antes de fazer o esboço no plano xy, vamos ver quais são as restrições sobre a função. Como a função é definida por um radical, temos que seu argumento deve ser não negativo, isto é:

Desta forma, o domínio de é o conjunto Para representá-lo, partimos do gráfico de . Em seguida fazemos uma reflexão em torno do eixo , que faz com que a expressão passe a ser , onde agora ao invés de . Em seguida fazemos uma translação de 10 unidades do grafico no eixo , dai a expressão se torna e o domínio passa a ser . Os processos estão indicados na figura a seguir:

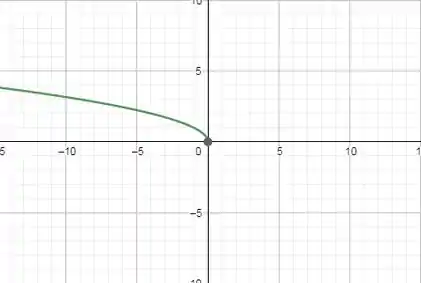
Reflexão:

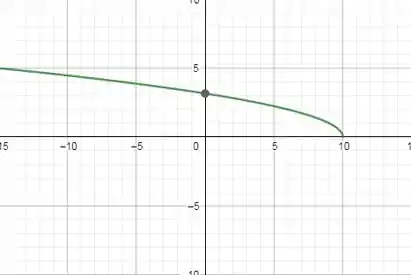
Translação:

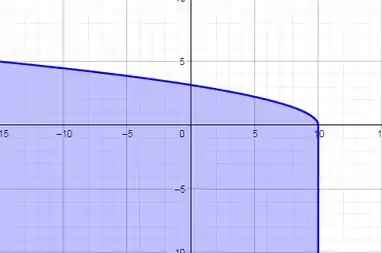
Como temos que e não , devemos tomar a parte abaixo do gráfico obtido, desta forma:

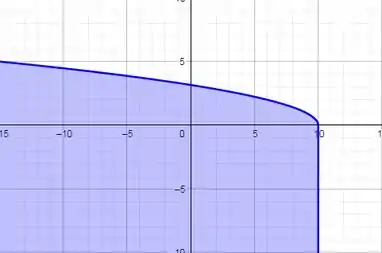
Agora vamos determinar a imagem de Como padrão, utilizamos:

Dito isso, temos que o menor valor que assume é , pois a função é definida por um radical, ou seja, é sempre maior que zero. Daí basta tomar ou . Temos também que não assume um valor máximo e para observar isso basta tomar e tomar , daí tem-se que . Logo .