Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.2 - Ex. 17
Seja
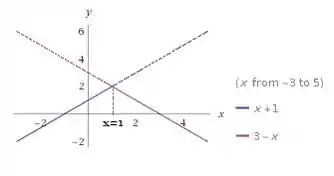
Esboce o gráfico de .
é derivável em ? Por quê?
Passo 1
Antes de temos que a função é uma reta crescente de coeficiente angular igual a (reta em azul). Para , a função toma a forma de uma reta decrescente de coeficiente angular (reta vermelha). Com a ajuda de um programa de geração de gráficos temos um esboço:
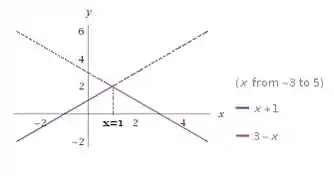
Em a função apresenta um bico e isso nos indica que nesse ponto a função não é derivável. Ara confirmar, vamos usar a definição de derivada
E fazer o teste para os limites bilaterais. Se ambos valores forem iguais, então a função é diferenciável. Caso contrário, não. Ok? Vamos lá?
Passo 2
Começando pela esquerda. Fazemos o limite para quando :
Agora simplificando ao máximo esse limite temos:
Show! Agora fazemos o mesmo processo, mas para a direita. Quando :
Agora simplificando ao máximo esse limite temos:
Opa! Como temos valores diferentes para os limites bilaterais, então essa função não é derivável em :
Resposta
