Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.2 - Ex. 14
Mostre que a função
Não é derivável em . Esboce o gráfico de .
Passo 1
Oi, galerinha! Para mostrar que a função não é derivável em , vamos usar a definição de derivada:
Bom, como aqui essa função é quebrada em temos que calcular o limite pela esquerda e pela direita e verificar se eles são iguais. Caso os limites sejam diferentes, significa que a função não é derivável naquele ponto.
Passo 2
Começando pela esquerda. Fazemos o limite para quando :
Agora simplificando ao máximo esse limite temos:
Show!
Passo 3
Agora fazemos o mesmo processo, mas para a direita. Quando :
Agora simplificando ao máximo esse limite temos:
Opa! Como temos valores diferentes para os limites bilaterais, então essa função não é derivável em :
Passo 4
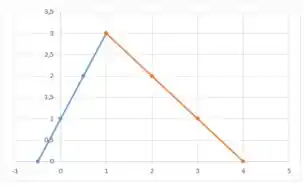
Vamos ao esboço? Bora lá!
Primeiro vamos olhar para a reta , para descobrir os pontos interessantes dessa reta vamos calcular e :
Agora escolhemos novos pontos e calculamos o :
Repara a escolha de já que para essa reta temos , ou seja não incluindo o , e como esperávamos tende a a medida que nos aproximamos de .
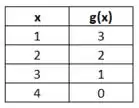
Agora vamos para a segunda função , aqui temos , vamos começar calculando esse ponto
é igual a como esperado. Agora vamos calcular , repara que não faz sentido calcular já que .
Calculamos mais alguns pontos:
Agora é a hora de jogar os dados no gráfico:
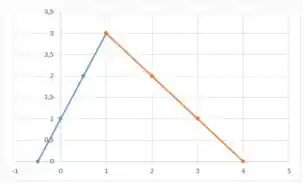
Em azul temos a reta que é crescente e tem coeficiente angular igual a . Em vermelho temos a reta que é decrescente e tem coeficiente angular igual a . Vemos que em há um bico e justamente nesse ponto a função não é derivável.
Resposta
