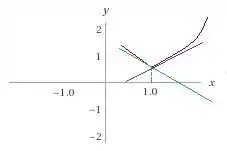
Dê exemplo (por meio de um gráfico) de uma função , definida e contínua em , tal que não exista.

O exercício pede uma função definida e contínua, mas que em a derivada não exista. Mas o que isso significa? Significa que em ela tem um bico! Dá uma espiada nesse gráfico aqui embaixo:

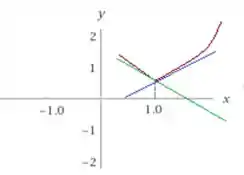
A função (em vermelho) está toda definida, até em . Mas antes desse ponto, a reta tangente é decrescente (em verde). E depois é crescente (em azul). Daí você se pergunta: mas isso não acontece com uma parábola no entorno da raiz? E você está certo! Acontece sim! Mas é suave! Aqui temos um bico, uma mudança “instantânea” na declividade da função. E lembrando que a derivada é a inclinação da reta tangente, num bico não temos como “equilibrar” uma reta, não é mesmo? Então ali, em a derivada não existe.